5a6b28d4-b7
UECE 2012 - Matemática - Circunferências e Círculos, Geometria Plana
Uma circunferência cuja medida do raio é 8 m
é dividida em sete arcos de comprimentos iguais.
Usando-se o valor 0,4338 para uma aproximação de
sen π/7, a medida, em metros, da distância entre as
extremidades de um destes arcos é um número
situado entre
Uma circunferência cuja medida do raio é 8 m
é dividida em sete arcos de comprimentos iguais.
Usando-se o valor 0,4338 para uma aproximação de
sen π/7, a medida, em metros, da distância entre as
extremidades de um destes arcos é um número
situado entre
A
6,93 e 6,94.
B
6,94 e 6,95.
C
6,95 e 6,96.
D
6,96 e 6,97.
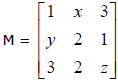
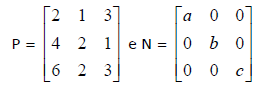 satisfazem a
igualdade M.N = P, então x + y + z é igual a
satisfazem a
igualdade M.N = P, então x + y + z é igual a então o conjunto imagem de f é
então o conjunto imagem de f é