Os valores de x , sendo 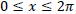 , para os quais as funções
, para os quais as funções 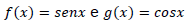 se interceptam, são
se interceptam, são
Os valores de x , sendo 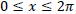 , para os quais as funções
, para os quais as funções 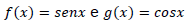 se interceptam, são
se interceptam, são





Os valores de x , sendo 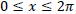 , para os quais as funções
, para os quais as funções 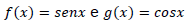 se interceptam, são
se interceptam, são





Dada a circunferência C : ( x-20)2 + (y-5)2 = 25, a equação da reta r, que contém a origem e é tangente à circunferência C no ponto A, conforme figura abaixo, é

y = 1/2 x
y = 8/15 x
y = 9/17 x
y = 2x
y = 1/2 x + 1
Sobre a reta s de equação y − 2x − 1= 0 e a circunferência C de equação x2 + y2 − 2x + y − 1= 0, afirma-se:
I. C tem centro no ponto O = (1, -1/2).
II. s é tangente a C.
III. s determina com o eixo das abscissas um ângulo θ tal que senθ = 2√5/5 .
Para essas afirmações, pode-se garantir que é verdadeira a alternativa

x2 + y2
- 4x - 2y + 7,5 = 0.
O número de soluções (p, q) do sistema
cos2 p - 2senq = 0
cos2 p + 2senq = 1,5
com p, q ∈ [- π, π], é

Após simplificar a expressão numérica
tg(1)tg(89) + tg(2)tg(88) + tg(3)tg(87) +...+ tg(10)tg(80),
obtemos:
Leia a observação: Sempre escrevemos sen(π) para significar seno de π radianos.
Sobre o valor de y , sendo y = sen(3) podemos dizer que: