6a993df3-e1
UCPEL 2011 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas
Para que a igualdade senx = 3n - 1 /2 seja verdadeira
para todo x, o valor de n deve pertencer ao intervalo
Para que a igualdade senx = 3n - 1 /2 seja verdadeira
para todo x, o valor de n deve pertencer ao intervalo
A
(-1/3,1)
B
[-1/3,1)
C
[-1/3,1]
D
(-1/3,1]
E
(1/3,1]
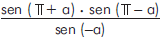 obtém-se
obtém-se 
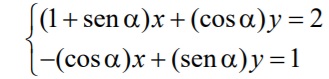
 é
solução do sistema
é
solução do sistema