Questõessobre Trigonometria
Em um parque de diversões, uma roda gigante de raio r = 10m, tendo
12 cadeiras igualmente espaçadas ao longo de seu perímetro, faz uma
volta completa em 30 segundos. Além disso, o ponto mais baixo atingido
ao longo do percurso circular está a 0,5m do solo. Certo dia, depois de
todos os assentos estarem ocupados, o assento 1 se encontrava na
posição indicada na figura, quando a roda começa a girar no sentido
anti-horário.

Sendo a distância desse assento ao solo, t segundos após a roda ter
começado a girar, dada pela expressão D(t) =M+N sen(αt), α > 0, é correto
afirmar que M − N é igual a

A temperatura da água de um tanque de criação de alevinos, quando
não artificialmente controlada, varia de acordo com a seguinte função matemática: F(t) = 21 − 4 . cos  , sendo t o tempo em horas
medido a partir das 6h da manhã de cada dia. Sabe-se que a temperatura ideal para a espécie criada é de 23°C. Supondo que não haja
um controle artificial da água, a temperatura ideal, em cada dia, será
atingida às:
, sendo t o tempo em horas
medido a partir das 6h da manhã de cada dia. Sabe-se que a temperatura ideal para a espécie criada é de 23°C. Supondo que não haja
um controle artificial da água, a temperatura ideal, em cada dia, será
atingida às:
 , sendo t o tempo em horas
medido a partir das 6h da manhã de cada dia. Sabe-se que a temperatura ideal para a espécie criada é de 23°C. Supondo que não haja
um controle artificial da água, a temperatura ideal, em cada dia, será
atingida às:
, sendo t o tempo em horas
medido a partir das 6h da manhã de cada dia. Sabe-se que a temperatura ideal para a espécie criada é de 23°C. Supondo que não haja
um controle artificial da água, a temperatura ideal, em cada dia, será
atingida às:Sendo f uma função definida por, f(x) = sen(x/2), 0 ≤ x ≤ 4π , então f (x) é positiva, quando:
Suponha que secα = x e
tgα
= x – 1, então x t em valor:
O valor da expressão tg 5π/3 - 3tg (-210°) é :
O valor da expressão tg 5π/3 - 3tg (-210°) é :
Sendo f uma função definida por f (x) = sen (x/2), 0 ≤ x ≤ 4π , então f (x) é positiva, quando:
Se cos x + sec (- x) = t, então, cos2 x + sec2 x é igual a:
t2 + 2
Considere os seguintes números complexos Z1 = -1 + j, Z2 = 2 - 2√3 j e Z3 = -√3 - j, em que
j é a unidade imaginária igual a√ −1 . São feitas as seguintes afirmações:

Assinale a alternativa correta:
Considere os seguintes números complexos Z1 = -1 + j, Z2 = 2 - 2√3 j e Z3 = -√3 - j, em que j é a unidade imaginária igual a√ −1 . São feitas as seguintes afirmações:

Assinale a alternativa correta:
O conjunto solução da equação sen(x) = cos[x-(π/2)] em IR é:
Uma circunferência tem centro (a, b) no primeiro quadrante,
raio r e é tangente aos eixos coordenados. Nessas condições, é
correto afirmar:
A equação (Sen x)2
– 5(Sen x) + 6 = 0
O número de soluções da equação 2cos x = sen x que pertencem ao intervalo [-16π/3, 16π/3] é:
Se 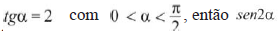 é igual a
é igual a
Se 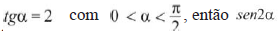 é igual a
é igual a
Considerando as expressões
M = sen4
x - cos4
x e N = 1 - 2cos2
x, é correto
afirmar que

As telhas onduladas de amianto, bastante populares, vêm tendo seu uso proibido em diversos
municípios brasileiros, por ser um material cancerígeno e por também poder causar doenças
respiratórias. Para substituí-las, podem ser usadas as chamadas ecotelhas — telhas onduladas
produzidas a partir da reciclagem de material plástico, como, por exemplo, aparas de tubos de
creme dental.
As ecotelhas têm elevada resistência mecânica, bem como à ação dos raios ultravioleta e
infravermelho, além de serem econômicas, são 100% impermeáveis.
Supondo-se que a curva representativa de uma secção transversal de uma telha ondulada, como
a da figura, seja definida por parte da função real f(x) = 1 − 2sen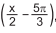 , é correto afirmar
que o conjunto-imagem e o período de f(x) são, respectivamente,
, é correto afirmar
que o conjunto-imagem e o período de f(x) são, respectivamente,

As telhas onduladas de amianto, bastante populares, vêm tendo seu uso proibido em diversos municípios brasileiros, por ser um material cancerígeno e por também poder causar doenças respiratórias. Para substituí-las, podem ser usadas as chamadas ecotelhas — telhas onduladas produzidas a partir da reciclagem de material plástico, como, por exemplo, aparas de tubos de creme dental.
As ecotelhas têm elevada resistência mecânica, bem como à ação dos raios ultravioleta e
infravermelho, além de serem econômicas, são 100% impermeáveis.
Supondo-se que a curva representativa de uma secção transversal de uma telha ondulada, como
a da figura, seja definida por parte da função real f(x) = 1 − 2sen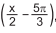 , é correto afirmar
que o conjunto-imagem e o período de f(x) são, respectivamente,
, é correto afirmar
que o conjunto-imagem e o período de f(x) são, respectivamente,
[−1, 3] e 4π.
Considerem-se os valores registrados na tabela T, obtidos em certo
experimento, que foram relacionados por meio de funções reais,
bijetoras, f e g.

Analisando-se as informações contidas em T, pode-se concluir que a
relação entre a e b é expressa por
Considerem-se os valores registrados na tabela T, obtidos em certo experimento, que foram relacionados por meio de funções reais, bijetoras, f e g.

Analisando-se as informações contidas em T, pode-se concluir que a relação entre a e b é expressa por
b = a
Considerem-se, no plano complexo representado na figura, os
pontos P, Q e R pertencentes a uma circunferência de centro na
origem.

Sendo P o afixo de 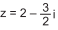 e QR, um arco medindo
e QR, um arco medindo 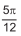 u.c.,
pode-se afirmar que o ponto R é afixo do número complexo que
pode ser representado, algebricamente, por
u.c.,
pode-se afirmar que o ponto R é afixo do número complexo que
pode ser representado, algebricamente, por
Considerem-se, no plano complexo representado na figura, os pontos P, Q e R pertencentes a uma circunferência de centro na origem.

Sendo P o afixo de 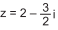 e QR, um arco medindo
e QR, um arco medindo 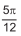 u.c.,
pode-se afirmar que o ponto R é afixo do número complexo que
pode ser representado, algebricamente, por
u.c.,
pode-se afirmar que o ponto R é afixo do número complexo que
pode ser representado, algebricamente, por





O valor de t, para que exista um ângulo x, sendo
que  é
é
O valor de t, para que exista um ângulo x, sendo
que  é
é