Questõessobre Trigonometria
Descrever essas informações, julgue o item seguinte.
O arco mede mais de 1,20 m.

O paralelepípedo reto-retângulo ABCDEFGH, representado
na figura, tem medida dos lados AB = 4, BC = 2 e BF = 2.

O seno do ângulo HÂF é igual a

O círculo a seguir tem o centro na origem do plano cartesiano xy e raio igual a 1. Nele, AP
determina um arco de 120°.

As coordenadas de P são:
O círculo a seguir tem o centro na origem do plano cartesiano xy e raio igual a 1. Nele, AP determina um arco de 120°.

As coordenadas de P são:
Uma escada de abrir, como a ilustrada abaixo,
tem suas laterais com comprimentos iguais a 1,4 m
cada. Nessas condições, a altura do topo da
escada em função do ângulo θ determinado no
interior da escada por suas laterais é expressa,
em metros, por


A função y = a + b cos x, com a e b reais, representada graficamente a seguir, intersecta o eixo y
no ponto de coordenadas (0, -1) e tem valor máximo y = 5. Qual é o valor da soma 5a + 2b?

A função y = a + b cos x, com a e b reais, representada graficamente a seguir, intersecta o eixo y no ponto de coordenadas (0, -1) e tem valor máximo y = 5. Qual é o valor da soma 5a + 2b?

Qual função trigonométrica representa o gráfico a seguir?

Qual função trigonométrica representa o gráfico a seguir?






Sabendo-se que cosx = -4/5 e x ∈ 2° quadrante, podemos afirmar que o valor de senx é
Uma circunferência tem centro no 1º quadrante, tangencia os eixos
cartesianos e passa pelo ponto de coordenadas (1, 2).
Um possível valor de seu raio é:
Sabemos que x ∈ (0, π/2 ) e que tg(x) =5/12.
Quanto vale sen(x)?
Ao resolver a equação sen4x=1, obtém-se como resultado
A variação da pressão sanguínea (em mmHG) de uma pessoa em função do tempo (em segundos) é uma função trigonométrica cuja lei é dada por:
P(t) = 100 − 20. cos(8π/3 t)
De acordo com os dados acima, assinale a alternativa que corresponde à CORRETA variação da pressão.
A variação da pressão sanguínea (em mmHG) de uma pessoa em função do tempo (em segundos) é uma função trigonométrica cuja lei é dada por:
P(t) = 100 − 20. cos(8π/3 t)
De acordo com os dados acima, assinale a alternativa que corresponde à CORRETA variação da pressão.
Sabemos que x ∈(0, π/2 ) e que tg(2x)= 4/3 .
Quanto vale tg(x)?
Quanto vale a soma abaixo?
cos(0)+cos(π)+cos(2π)+cos(3π)+cos(4π)+cos(5π)+cos(6π)
Quanto vale a soma abaixo?
cos(0)+cos(π)+cos(2π)+cos(3π)+cos(4π)+cos(5π)+cos(6π)

Em uma determinada região litorânea, a maré oscila segundo a função h(t) = 3 – 2sen( πt/
12 ), sendo h a altura em
metros, que a maré atinge no tempo t em horas, medido a
partir de 6h da manhã. Uma embarcação, que se encontra
encalhada às 11h da manhã, precisa de uma profundidade
mínima de 2 metros para navegar. Assinale a alternativa que
apresenta quantas horas os tripulantes dessa embarcação ainda
terão que esperar para prosseguirem viagem.
Admitindo-se que o peso de determinada pessoa, ao longo de uma ano, possa ser
modelado pela função P(t) = 65 − 5cos  , em que t =1,...,12 corresponde aos
meses de janeiro a dezembro e considerando √3 = 1,7, pode-se estimar que, de maio
até agosto, o peso dessa pessoa
, em que t =1,...,12 corresponde aos
meses de janeiro a dezembro e considerando √3 = 1,7, pode-se estimar que, de maio
até agosto, o peso dessa pessoa
 , em que t =1,...,12 corresponde aos
meses de janeiro a dezembro e considerando √3 = 1,7, pode-se estimar que, de maio
até agosto, o peso dessa pessoa
, em que t =1,...,12 corresponde aos
meses de janeiro a dezembro e considerando √3 = 1,7, pode-se estimar que, de maio
até agosto, o peso dessa pessoaUm avião levanta voo sob um ângulo de 30°. Então, depois que tiver percorrido 500 m, conforme indicado na
figura, sua altura h em relação ao solo, em metros, será igual a:
Considere sen 30° = 0,50 ou cos 30° = 0,87.


O conjunto-imagem da função f definida por f(x) = sen (x) + h é [ -2; 0 ]. O valor de h é
Sabendo que 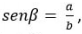 com
com 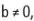 um possível valor para
um possível valor para 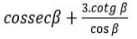 é
é
Sabendo que 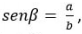 com
com 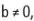 um possível valor para
um possível valor para 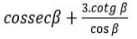 é
é