Questõesde UNEMAT sobre Triângulos

No triângulo equilátero ABC, os pontos M e N são respectivamente pontos médios dos lados .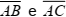

O segmento 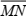mede 6 cm.

A área do triângulo ABC mede:

Na figura abaixo, o triângulo ABC é um triângulo equilátero de 3 cm de lado, e o triângulo retângulo BCD tem lados BD = 4 cm e CD = 5 cm e 0 90 .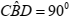

Qual a medida do segmento AD ?

Conforme ilustra a figura abaixo, os triângulos ABC e CDB estão inscritos em um círculo de diâmetro d.

Sabendo-se que o ângulo α mede 50º e que a medida do segmento CD é igual ao diâmetro d do círculo, assinale a alternativa que corresponde à medida (em graus) do ângulo β.

Uma sequência infinita de triângulos equiláteros pode ser construída inscrevendo um triângulo dentro do outro, a partir do primeiro.

Na figura abaixo estão ilustrados os três primeiros triângulos equiláteros dessa sequência.

Sabendo-se que o primeiro triângulo dessa sequência (triângulo ABC) tem lados medindo 3 cm, e que as medidas dos lados dos triângulos inscritos são iguais à metade da medida do lado do triângulo que o inscreve, assinale a alternativa que apresenta o valor da soma das áreas dos triângulos desta sequência infinita.

Um topógrafo deseja medir a distância entre dois pontos (A e C), situados em margens opostas de um rio. Para isso, ele escolheu um ponto B, à 80m do ponto C, com o qual ele obteve os ângulos α = 60° e β = 30°, indicados na figura abaixo.

De acordo com a figura, assinale a alternativa que corresponde à distância (em metros) do ponto A ao ponto C, considerando √3 = 1,73.