f5702a5e-d9
FAMERP 2019 - Matemática - Geometria Plana, Triângulos
Em um plano cartesiano, dois vértices de um triângulo equilátero estão sobre a reta de equação y = 2x – 2. O terceiro
vértice desse triângulo está sobre a reta de equação y = 2x + 2.
A altura desse triângulo, na mesma unidade de medida dos
eixos cartesianos ortogonais, é igual a
Em um plano cartesiano, dois vértices de um triângulo equilátero estão sobre a reta de equação y = 2x – 2. O terceiro
vértice desse triângulo está sobre a reta de equação y = 2x + 2.
A altura desse triângulo, na mesma unidade de medida dos
eixos cartesianos ortogonais, é igual a
A
4√3 / 5
B
3√3 / 4
C
2√5 / 5
D
4√5 / 5
E
√3/2
 , e . Com base nessas informações, é
, e . Com base nessas informações, é



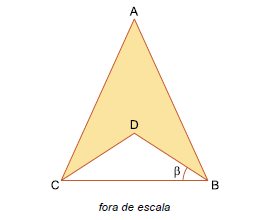
 mede 30 . Os segmentos
mede 30 . Os segmentos  são, respectivamente, a altura e a mediana relativas ao vértice A.
Os segmentos
são, respectivamente, a altura e a mediana relativas ao vértice A.
Os segmentos  são, respectivamente, as bissetrizes dos ângulos
são, respectivamente, as bissetrizes dos ângulos 
 mede:
mede:
 mede
120º, AD = 2 cm e CD = 4 cm. Nessas condições, pode-se afirmar
que a área do quadrilátero ABCD é igual a:
mede
120º, AD = 2 cm e CD = 4 cm. Nessas condições, pode-se afirmar
que a área do quadrilátero ABCD é igual a:




