Analise as afirmações a seguir.
I No triângulo MON , as medidas são indicadas
em centímetros.

Se OP é bissetriz do ângulo MÔN, então a
medida do lado MN é 42 cm.
II Numa progressão aritmética crescente de 51
termos, a3 + a49 = 198 e a5 + a47 = k . Então, o valor de k /9 é 22.
III Para ser classificado para a última fase de um
concurso público um candidato deve atingir
nota superior ou igual a 7,00 na média ponderada de suas três primeiras avaliações. As
notas de Jonas foram 5,50; 6,80 e 7,70 e os
pesos das avaliações são, respectivamente, 1,
2 e 3. Portanto, Jonas não foi classificado para
última fase.
IV Determinado medicamento manipulado é
constituído somente de três elementos: substância A (2mL), substância B (3mL) e água,
totalizando 10ml de medicamento. Para melhorar o efeito do medicamento, é indicado
dobrar a quantidade da substância A mantendo as quantidades das demais. Dessa forma,
a nova mistura será constituída de 40% da
substância A.
Todas as afirmações corretas estão em:






 e
e  são paralelos.
são paralelos.
 = 10 m,
= 10 m,  =6m e
=6m e  =12m ,
então o comprimento de
=12m ,
então o comprimento de  é:
é:











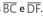 .
Se BE = 2; CE, EF = 2; DE, AB = 4 cm e
AD = 9 cm, qual das medidas a seguir
mais se aproxima de CF?
.
Se BE = 2; CE, EF = 2; DE, AB = 4 cm e
AD = 9 cm, qual das medidas a seguir
mais se aproxima de CF?