163258d7-02
UECE 2018 - Matemática - Álgebra Linear, Sistemas Lineares
Se o sistema de equações  Onde a = sen α e b = cos α, admite uma única
solução, então, pode-se afirmar corretamente que
Onde a = sen α e b = cos α, admite uma única
solução, então, pode-se afirmar corretamente que
Se o sistema de equações  Onde a = sen α e b = cos α, admite uma única
solução, então, pode-se afirmar corretamente que
Onde a = sen α e b = cos α, admite uma única
solução, então, pode-se afirmar corretamente que
 Onde a = sen α e b = cos α, admite uma única
solução, então, pode-se afirmar corretamente que
Onde a = sen α e b = cos α, admite uma única
solução, então, pode-se afirmar corretamente queA
2 α ≠ k π, onde k é um número inteiro.
B
α = k π, onde k é um número inteiro.
C
α = (2k + 1) π, onde k é um número inteiro.
D
2 α ≠ 1 + k π, onde k é um número inteiro.
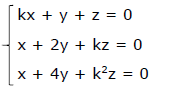
 pode-se afirmar corretamente que
pode-se afirmar corretamente que