Dado o sistema de equação:
Nas condições em que x > 0 e y > 0 , calcule o valor de z , em
que xz = y
Durante uma festa de colégio, um grupo de alunos organizou uma rifa. Oitenta alunos faltaram à festa e não participaram da rifa. Entre os que compareceram, alguns compraram três bilhetes, 45 compraram 2 bilhetes, e muitos compraram apenas um. O total de alunos que comprou um único bilhete era 20% do número total de bilhetes vendidos, e o total de bilhetes vendidos excedeu em 33 o número total de alunos do colégio.
Quantos alunos compraram somente um bilhet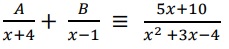e?
é:Considere o seguinte sistema:
Na solução desse sistema, tem-se x = a e y = b. Assim, o valor da
expressão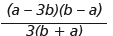 
é
Médicos alertam sobre a importância de educar as crianças para terem hábitos alimentares saudáveis. Por exemplo, analisando-se uma bolacha com recheio de chocolate (25 g) e um pé de alface (25 g), observam-se as seguintes quantidades de nutrientes, respectivamente:
• carboidratos: 15 g e 0,5 g;
• proteínas: 1,9 g e 0,5 g.
Disponível em: http://veja.abril.com.br. Acesso em: 27 abr. 2010 (adaptado).
Considerando as informações apresentadas, qual deve
ser o número de pés de alface consumidos para se obter
a mesma quantidade de carboidratos de uma bolacha?
Sabendo que k é um número real, considere o sistema linear nas variáveis reais x e y,
É correto afirmar que esse sistema
Seja a função h(x) definida para todo número real x por
Então, h(h(h(0))) é igual a
Um grupo de estudantes fará uma excursão e alugará ônibus para transportá-lo. A transportadora dispõe de ônibus em dois tamanhos, pequeno e grande. O pequeno tem capacidade para 24 pessoas, ao custo total de R$ 500,00. O grande tem capacidade para 40 pessoas, ao custo total de R$ 800,00. Sabe-se que pelo menos 120 estudantes participarão da excursão e que o grupo não quer gastar mais do que R$ 4.000,00 com o aluguel dos ônibus.
Sendo x o número de ônibus pequenos e y o número de ônibus grandes que serão alugados, o par ordenado (x, y) terá que pertencer, necessariamente, ao conjunto solução do sistema de inequações
O acesso aos terminais eletrônicos do banco em que o senhor e a senhora Euler têm conta conjunta é feito através de um código de acesso que consiste de um conjunto de três pares de letras que devem ser informados numa ordem pré-estabelecida. Como as letras do seu código eram todas anteriores à letra J, o casal associou algarismos a elas e memorizou seu código pelos números formados por cada par de algarismos. Por exemplo, se o código do casal fosse AB BA DC, ele teria sido memorizado pelos números 12, 21 e 43.
Certo dia, a senhora Euler recebeu um telefonema do seu esposo solicitando o código, uma vez que ele havia esquecido. Senhora Euler, precavida, enviou a seguinte mensagem: a soma dos três é igual a 84; o primeiro é o triplo do segundo; o segundo é a metade do terceiro.
Considere o sistema linear nas variáveis reais x , y , z e w ,
Logo, a soma x + y + z + w é igual a