Para que o sistema linear 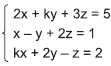 não tenha solução, o valor
da constante k deverá ser
não tenha solução, o valor
da constante k deverá ser
Para que o sistema linear 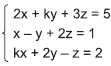 não tenha solução, o valor
da constante k deverá ser
não tenha solução, o valor
da constante k deverá ser
Para que o sistema linear 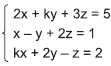 não tenha solução, o valor
da constante k deverá ser
não tenha solução, o valor
da constante k deverá ser
Em relação ao sistema  pode-se afirmar corretamente que
pode-se afirmar corretamente que
Considere a solução (x,y) do sistema
sen(x + y) = √3/2
tg(x + y) = √3/3
onde os valores x e y, expressos em radianos, são os menores valores positivos possíveis. Nestas condições a soma x2 + y2 é igual a
O sistema  é homogêneo e tem infinitas
soluções. Os valores reais de m, p e q são, nesta ordem:
é homogêneo e tem infinitas
soluções. Os valores reais de m, p e q são, nesta ordem:
Se t ∈R e i = √−1, as equações paramétricas  representam:
representam:
Considere o sistema de equações lineares:

Pode-se afirmar que a expressão logy x+logx y é
igual a:
Para que o sistema linear
x + 2y - 3z = a
{ 2x + 6y - 11z = b
x - 2y + 7z = 0
tenha solução, é necessário que
É CORRETO afirmar que a solução do sistema
Assinale a alternativa que indica para quais valores
de m o sistema de equações lineares 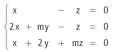 é possível e indeterminado.
é possível e indeterminado.
O sistema  é:
é:
Se f : R2 → R é a função definida por f(x, y) = 
pode-se concluir que ∂f/ ∂x ( 1, 1) = 7.


A rodovia BA-99 que liga a cidade de Lauro de Freitas-BA ao litoral norte da Bahia, possui um posto telefônicoa cada 2 km. Considerando esta informação, analise as seguintes afirmações:
I. Se um carro parar nessa estrada, a distância máxima que este carro possui de algum posto telefônico é de 2 km.
II. Se um carro parar nessa estrada, a distância máxima que este carro possui de algum posto telefônico é maiorque 2 km.
III. Se um carro parar nessa estrada, a distância máxima que este carro possui de algum posto telefônico é de 1 km.
IV. A função “distância” do carro que dá a distância mais próxima de um posto telefônico pode ser escritada forma:  , sendo x a distância percorrida em km em relação ao último postotelefônico que o carro passou.
, sendo x a distância percorrida em km em relação ao último postotelefônico que o carro passou.
Considere os números complexos:

Então, sobre o produto y . (-ix), podemos afirmar que:
Sobre o sistema de equações lineares  é CORRETO afirmar que
é CORRETO afirmar que
Dado o sistema , em que a e b são números reais, assinale a alternativa correta.
, em que a e b são números reais, assinale a alternativa correta.
Chama-se solução trivial de um sistema linear aquela em que todos os valores
das incógnitas são nulos.
O sistema linear, nas incógnitas 
