8b1dfd37-60
UFLA 2008 - Matemática - Aritmética e Problemas, Sistemas de Numeração e Operações Fundamentais
Em 1787, um professor, para manter a classe ocupada, mandou que os alunos somassem todos os números inteiros de 1 até 100. Quase imediatamente um aluno de 10 anos, Gauss (mais tarde denominado o príncipe dos matemáticos), respondeu 5050. A idéia genial de sua solução foi:

Usando a mesma idéia, a soma

é igual a:
Em 1787, um professor, para manter a classe ocupada, mandou que os alunos somassem todos os números inteiros de 1 até 100. Quase imediatamente um aluno de 10 anos, Gauss (mais tarde denominado o príncipe dos matemáticos), respondeu 5050. A idéia genial de sua solução foi:

Usando a mesma idéia, a soma

é igual a:

Usando a mesma idéia, a soma

é igual a:
A

B

C

D

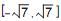 existem apenas
existem apenas







