No universo dos números reais, a equação  é satisfeita por apenas
é satisfeita por apenas
 é satisfeita por apenas
é satisfeita por apenas é satisfeita por apenas
é satisfeita por apenasO número 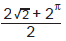 pertence ao intervalo:
pertence ao intervalo:
O quadro apresenta a ordem de colocação dos seis primeiros países em um dia de disputa nas Olimpíadas. A ordenação é feita de acordo com as quantidades de medalhas de ouro, prata e bronze, respectivamente.

Se as medalhas obtidas por Brasil e Argentina fossem
reunidas para formar um único país hipotético, qual a
posição ocupada por esse país?
O gerente de um estacionamento, próximo a um grande aeroporto, sabe que um passageiro que utiliza seu carro nos traslados casa-aeroporto-casa gasta cerca de R$ 10,00 em combustível nesse trajeto. Ele sabe, também, que um passageiro que não utiliza seu carro nos traslados casa-aeroporto-casa gasta cerca de R$ 80,00 com transporte.
Suponha que os passageiros que utilizam seus próprios veículos deixem seus carros nesse estacionamento por um período de dois dias.
Para tornar atrativo a esses passageiros o uso do
estacionamento, o valor, em real, cobrado por dia de
estacionamento deve ser, no máximo, de
O veículo terrestre mais veloz já fabricado até hoje é o Sonic Wind LSRV, que está sendo preparado para atingir a velocidade de 3 000 km/h. Ele é mais veloz do que o Concorde, um dos aviões de passageiros mais rápidos já feitos, que alcança 2 330 km/h.

Para uma distância fixa, a velocidade e o tempo são inversamente proporcionais.
BASILIO, A. Galileu, mar. 2012 (adaptado).
Para percorrer uma distância de 1 000 km, o valor mais próximo da diferença, em minuto, entre os tempos
gastos pelo Sonic Wind LSRV e pelo Concorde, em suas
velocidades máximas, é
Sob a orientação de um mestre de obras, João e Pedro trabalharam na reforma de um edifício. João efetuou reparos na parte hidráulica nos andares 1, 3, 5, 7, e assim sucessivamente, de dois em dois andares. Pedro trabalhou na parte elétrica nos andares 1,4, 7, 10, e assim sucessivamente, de três em três andares. Coincidentemente, terminaram seus trabalhos no último andar. Na conclusão da reforma, o mestre de obras informou, em seu relatório, o número de andares do edifício. Sabe-se que, ao longo da execução da obra, em exatamente 20 andares, foram realizados reparos nas partes hidráulica e elétrica por João e Pedro.
Qual é o número de andares desse edifício?
O ábaco é um antigo instrumento de cálculo que usa notação posicional de base dez para representar números naturais. Ele pode ser apresentado em vários modelos, um deles é formado por hastes apoiadas em uma base. Cada haste corresponde a uma posição no sistema decimal e nelas são colocadas argolas; a quantidade de argolas na haste representa o algarismo daquela posição. Em geral, colocam-se adesivos abaixo das hastes com os símbolos U, D, C, M, DM e CM que correspondem, respectivamente, a unidades, dezenas, centenas, unidades de milhar, dezenas de milhar e centenas de milhar, sempre começando com a unidade na haste da direita e as demais ordens do número no sistema decimal nas hastes subsequentes (da direita para esquerda), até a haste que se encontra mais à esquerda.
Entretanto, no ábaco da figura, os adesivos não seguiram a disposição usual.

Nessa disposição, o número que está representado na
figura é

Uma família deseja organizar todas as fotos de uma viagem em um álbum com determinado número de páginas, sem sobra de fotos ou de páginas. Para isso, foram testados dois critérios de organização.
O primeiro critério, que consistia na colocação de uma única foto em cada página, foi descartado, uma vez que sobraram 50 fotos.
Com a adoção do segundo critério, a de uma única foto em algumas páginas e de três fotos nas demais, não sobraram fotos nem páginas, e o objetivo da família foi alcançado.
O número total de páginas em que foram colocadas três fotos é igual a:

Uma rede é formada de triângulos equiláteros congruentes, conforme a representação abaixo.

Uma formiga se desloca do ponto A para o ponto B sobre os lados dos triângulos, percorrendo X caminhos distintos, cujos comprimentos totais são todos iguais a d.
Sabendo que d corresponde ao menor valor possível para os comprimentos desses caminhos, X
equivale a:
Uma calculadora tem duas teclas especiais, A e B. Quando a tecla A é digitada, o número que está no visor é substituído pelo logaritmo decimal desse número. Quando a tecla B é digitada, o número do visor é multiplicado por 5.
Considere que uma pessoa digitou as teclas BAB, nesta ordem, e obteve no visor o número 10.
Nesse caso, o visor da calculadora mostrava inicialmente o seguinte número:
TEXTO 7
A gota que fez transbordar a caixa da paciência de vovó foi um casalzinho folgado. Cansada da algazarra, do som da sanfona, que por três dias e três noites vinha balançando os alicerces da Casa, vovó foi procurar refúgio na paz de seu quarto. Que paz que nada, ali também a festa rolava solta. Abismada, ela viu um casalzinho iniciando sua lua de mel, imaginem onde? Na cama de vovó! Pena que o urinol estivesse vazio. Furiosa, Ana Vitória pensou em apelar para o chicote. Depois seu pensamento voltou para os primeiros dias de seu casamento, lembrou-se da urgência que a fazia deixar tudo por fazer e ir atrás do marido no roçado. Viu a si mesma, viu os dois, ela e o marido, um casal corado e feliz se deitando debaixo de qualquer árvore. Dez meses após o casamento nasceu o primeiro filho, seguido de outros, um por ano. A leveza daquele início parecia tão distante, tão irreal. Uma lagrimazinha de saudade marejou seus olhos abatidos, rolou pela face cansada e foi morrer no peito murcho. Desanimada, ela pensou que nunca mais ia parar de ter filhos, de lavar bundinhas melecadas de cocô. Acabou deixando os pombinhos em paz, eles que aproveitassem a vida enquanto era possível. Mas avisou aos interessados que preferia perder um bom quinhão de suas terras a continuar convivendo com tamanha barafunda. Assim, a ideia remota da criação de um arraial foi posta em prática. Doações foram feitas e o terreno demarcado.
As construções começaram a nascer com a rapidez dos cogumelos. Primeiro a igreja com a torre central, beiral duplo em madeira recortada em bicos. Paredes azuis, janelas brancas. Feinha a pobre igreja, mas nem por isso desprezada. Talvez sua maior virtude estivesse na singeleza, no aconchego. A igrejinha era o orgulho do povoado. Sobre o altar feito por um carpinteiro caprichoso, a imagem de um Cristo cansado, a cabeça pensa, o olhar vazio. Descascado, ensanguentado, provocava nos fieis uma piedade quase dolorosa. Foi nessa igreja que meus pais me apresentaram ao Nosso Criador.
(BARROS, Adelice da Silveira. Mesa dos inocentes. Goiânia: Kelps, 2010. p. 74-75.)