Fabiana Murer garante mais uma medalha de ouro
na Noruega. A atleta brasileira saltou 4,60 m na etapa da
Diamond League e terminou em primeiro lugar na disputa.
Ela ainda é detentora da melhor marca do ano. Ao final da
prova, a classificação dos quatro melhores resultados foi:
1° lugar: Fabiana Murer (BRA) - 4,60 m
2° lugar: Aleksandra Kiryashiva (RUS) - 4,50 m
3° lugar: Anna Rogowska (POL) - 4,40 m
4° lugar: Monika Pyrek (POL) - 4,30 m
Disponível em: http://www.globoesporte.globo.com. Acesso em: 24 jun. 2011 (adaptado).
A diferença entre as marcas da 1a e da 4a colocadas
pode ser comparada com a altura de um animal adulto.
Que animal é esse?
Fabiana Murer garante mais uma medalha de ouro na Noruega. A atleta brasileira saltou 4,60 m na etapa da Diamond League e terminou em primeiro lugar na disputa. Ela ainda é detentora da melhor marca do ano. Ao final da prova, a classificação dos quatro melhores resultados foi:
1° lugar: Fabiana Murer (BRA) - 4,60 m
2° lugar: Aleksandra Kiryashiva (RUS) - 4,50 m
3° lugar: Anna Rogowska (POL) - 4,40 m
4° lugar: Monika Pyrek (POL) - 4,30 m
Disponível em: http://www.globoesporte.globo.com. Acesso em: 24 jun. 2011 (adaptado).
A diferença entre as marcas da 1a e da 4a colocadas pode ser comparada com a altura de um animal adulto. Que animal é esse?












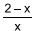 é
é





