Questõessobre Relações Métricas no Triângulo Retângulo

InícioTodas as questões
1
1
Foram encontradas 57 questões
bf6f71a2-07
UNICENTRO 2016 - Matemática - Relações Métricas no Triângulo Retângulo, Geometria Plana

Um homem coloca-se em um ponto A e observa o topo de um poste, sob um ângulo de 30º. Anda 12 metros na direção do poste, alcançando o ponto B, de onde vê o topo do poste sob um ângulo de 45º.
A altura desse poste, em metros, é

A
6(1 + √3)
B
3(1 + √3)
C
(3 + √3)
D
(1 + √3)
621f0700-ff
URCA 2017 - Matemática - Relações Métricas no Triângulo Retângulo, Geometria Plana

Seja ABC um triângulo retângulo, reto em A. Seja h a altura de ABC relativa ao lado BC. Se os catetos medem 3√2cm e 4√2cm, a altura h mede?

A
3√2/5 cm
B
12√10/5 cm
C
6√5/5 cm
D
12√2/5 cm
E
6√10/5 cm
6b5ca575-01
MACKENZIE 2019 - Matemática - Relações Métricas no Triângulo Retângulo, Geometria Plana

Na figura acima, ABC e BCD são triângulos retângulos. Se sen θ = 2/3 e AB mede 18 m, então o segmento BD mede


A
6 m
B
8 m
C
10 m
D
12 m
E
14 m
4d000140-fd
ESPM 2018 - Matemática - Relações Métricas no Triângulo Retângulo, Geometria Plana

Num triângulo retângulo de hipotenusa a e catetos b e c, a medida da altura relativa à hipotenusa é igual a 4. O valor da expressão a/b · c + b/a · c + c/a · b é igual a:

A
1
B
2
C
1/2
D
1/4
E
1/8
424bf7e9-f7
UNEMAT 2015 - Matemática - Relações Métricas no Triângulo Retângulo, Geometria Plana

Para medir a altura de uma torre um professor de Matemática recorreu à semelhança de triângulos. Em um dia ensolarado cravou uma estaca de madeira em um terreno plano próximo à torre, de modo que a estaca formasse um ângulo de 90° com o solo plano. Em determinado momento mediu a sombra produzida pela torre e pela estaca no solo plano; constatou que a sombra da torre media 12 m e a sombra da estaca 50 cm.

Se a altura da estaca é de 1 metro a partir da superfície do solo, qual a altura da torre?

A
60 metros.
B
24 metros.
C
6 metros.
D
600 metros.
E
240 metros.
d2a1ca63-8c
UNICAMP 2021 - Matemática - Relações Métricas no Triângulo Retângulo, Progressão Geométrica - PG, Geometria Plana, Progressões

Considere que as medidas dos lados de um triângulo retângulo estão em progressão geométrica. Sendo a a medida do menor lado e A a área desse triângulo, é correto afirmar que

A
B
C
D
cd5cf4dd-eb
ULBRA 2010 - Matemática - Relações Métricas no Triângulo Retângulo, Geometria Plana

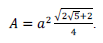
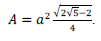
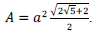
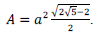
Desde o início de uma obra (em sua demarcação inicial), até o acabamento final (durante a colocação dos pisos), os pedreiros necessitam obter ângulos retos. O pedreiro, ao marcar 45 cm e 60 cm em duas laterais de paredes que se interceptam e, depois, unir esses pontos para encontrar uma medida equivalente a 75 cm, utiliza, muitas vezes mesmo sem ter conhecimento, um teorema matemático. O que, na linguagem dos pedreiros é chamado de “deixar no esquadro”, equivale a uma aplicação do:

A
Teorema de Tales.
B
Teorema de Pitágoras.
C
Teorema de Pascal.
D
Teorema das Raízes Racionais.
E
Teorema Fundamental da Álgebra.
de8efffd-7b
USP 2021 - Matemática - Relações Métricas no Triângulo Retângulo, Polígonos, Geometria Plana

Um marceneiro possui um pedaço de madeira no formato de um triângulo retângulo, cujos catetos medem 12 cm e 35 cm. A partir desta peça, ele precisa extrair o maior quadrado possível, de tal forma que um dos ângulos retos do quadrado coincida com o ângulo reto do triângulo. A medida do lado do quadrado desejado pelo marceneiro está mais próxima de

A
8,0 cm.
B
8,5 cm.
C
9,0 cm.
D
9,5 cm.
E
10,0 cm.
6bcdfa74-fc
ENCCEJA 2018 - Matemática - Álgebra Linear - Equações Lineares, Espaço Vetorial e Transformações Lineares e Matrizes, Relações Métricas no Triângulo Retângulo, Geometria Plana, Triângulos, Álgebra Linear

Um caminhoneiro viajando pelo interior de seu país chega à cidade A. No tanque de combustível do seu veículo restam somente 10 litros. Seu destino final é a cidade D e as distâncias entre cada uma das cidades A, B, C e D são as indicadas na figura. Somente existem postos de abastecimento nas cidades C e D. O veículo consegue percorrer 5 quilômetros (km) com um litro de combustível.



Desejando fazer o percurso mais curto possível, mas sem ficar parado no caminho, o trajeto que ele terá que escolher para ir de A até D e a distância a ser percorrida serão, respectivamente,

A
ABD e 60 km.
B
ACD e 100 km.
C
ABCD e 120 km.
D
ACBD e 140 km.
ba1e84a2-fb
FGV 2012 - Matemática - Relações Métricas no Triângulo Retângulo, Geometria Plana

Em um triângulo retângulo ABC, o cateto AB mede o triplo do cateto BC e α é a medida do ângulo interno relativo ao vértice A.


O valor de cos(2α) é

A
0,8
B
0,7
C
0,6
D
0,5
E
0,4
a3ee48f7-f2
IFAL 2016 - Matemática - Circunferências e Círculos, Relações Métricas no Triângulo Retângulo, Geometria Plana

Calcule o valor de m na figura:



Onde C é o centro do círculo de raio 10.


A
1.
B
2.
C
3.
D
4.
E
5.
7fd5f9a4-b0
UNEMAT 2017 - Matemática - Análise de Tabelas e Gráficos, Pontos e Retas, Relações Métricas no Triângulo Retângulo, Geometria Analítica, Geometria Plana

Na figura abaixo, o segmento AB é a hipotenusa de um triângulo retângulo isósceles ACB, retângulo em C, e mede 4√2.



Sabendo que as coordenadas do ponto A são (-1,1), e que a abscissa do ponto C é positiva, as coordenadas de C são:

A
(3, -3)
B
(3,1)
C
(-1,5)
D
(−1 + 4√2, 1)
E
(-5,5)
ebcaa768-dc
FAMEMA 2017 - Matemática - Relações Métricas no Triângulo Retângulo, Polígonos, Geometria Plana, Triângulos

A figura mostra um quadrado ABCD, com 6 cm de lado, e um triângulo retângulo ABF de hipotenusa  , com o ponto F no prolongamento do lado  e o ponto E sendo a intersecção dos segmentos  e .

Sabendo que o ângulo FÂB mede 60º, a medida do segmento  é 

A
(√3 + 3) cm.
B
(2√3+3) cm.
C
2(3+√3) cm.
D
2√3 cm.
E
2(3-√3) cm.
1859dd7b-e6
FAG 2019 - Matemática - Relações Métricas no Triângulo Retângulo, Geometria Plana

Na figura, o triângulo ABC é retângulo em A e AM é bissetriz do ângulo A.



Se AC = 3 e AM = √2, então, a medida da hipotenusa BC é

A
3√2
B
(3√ 5)/2
C
(5√ 3)/2
D
(2√ 3)/5
E
3 √28/2
923d2ff3-ea
IF Sul Rio-Grandense 2016 - Matemática - Relações Métricas no Triângulo Retângulo, Geometria Plana

As raízes das equações 5x - 2 = 3x + 6 e (y - 1).(y + 4) = y2 + 5 representam as medidas dos comprimentos dos catetos do triângulo retângulo da figura, representada ao lado.



Assim, o comprimento da hipotenusa z desse triângulo retângulo é

A
4
B
5
C
6
D
7
115d9e2b-dd
UEM 2011, UEM 2011 - Matemática - Relações Métricas no Triângulo Retângulo, Geometria Plana

Se o ângulo do vértice B mede 35 °, o ângulo do vértice C mede 65°.

MATEMÁTICA - Formulário


Dado um triângulo ABC, retângulo em A, sejam h, a e b as medidas, em unidades de comprimento, dos lados BC, AB e AC, respectivamente. Em relação ao exposto, assinale o que for correto.

C
Certo
E
Errado
1166d8da-dd
UEM 2011, UEM 2011 - Matemática - Relações Métricas no Triângulo Retângulo, Geometria Plana

Se θ é o ângulo de vértice C, cosθ = 1/2 e h = 20, então b =10.

MATEMÁTICA - Formulário


Dado um triângulo ABC, retângulo em A, sejam h, a e b as medidas, em unidades de comprimento, dos lados BC, AB e AC, respectivamente. Em relação ao exposto, assinale o que for correto.

C
Certo
E
Errado
f40cec87-dd
MACKENZIE 2017 - Matemática - Relações Métricas no Triângulo Retângulo, Geometria Plana


Na figura acima, ABC é um triângulo retângulo. A altura relativa ao vértice A encontra o lado BC no ponto D tal que = 1/2 . Se = 12cm, as áreas dos triângulos ABD e ADC, em cm2, são respectivamente

A
2√2 e 4√2
B
4√2 e 8√2
C
4√3 e 8√3
D
8√2 e 16√2
E
8√3 e 16√3
4c066de5-d7
FGV 2013 - Matemática - Relações Métricas no Triângulo Retângulo, Geometria Plana

Um triângulo ABC é retângulo em A . Sabendo que BC = 5 e ABC = 30°, pode-se afirmar que a área do triângulo ABC é:

A
3,025√3
B
3,125√3
C
3,225√3
D
3,325√3
E
3,425√3
de2096fb-b9
UECE 2016 - Matemática - Relações Métricas no Triângulo Retângulo, Polígonos, Geometria Plana

No triângulo UVW, retângulo em V, a medida da hipotenusa UW é duas vezes a medida do cateto VW. Assim, pode-se afirmar corretamente que a medida em graus do ângulo VÛW é

A
30.
B
60.
C
40.
D
45.