De acordo com a Lei Universal da Gravitação, proposta
por Isaac Newton, a intensidade da força gravitacional F
que a Terra exerce sobre um satélite em órbita circular
é proporcional à massa m do satélite e inversamente
proporcional ao quadrado do raio r da órbita, ou seja,

No plano cartesiano, três satélites, A, B e C, estão
representados, cada um, por um ponto (m ; r) cujas
coordenadas são, respectivamente, a massa do satélite
e o raio da sua órbita em torno da Terra.

Com base nas posições relativas dos pontos no
gráfico, deseja-se comparar as intensidades FA, FB e FC da força gravitacional que a Terra exerce sobre os satélites
A, B e C, respectivamente.
As intensidades FA, FB e FC expressas no gráfico
satisfazem a relação




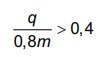
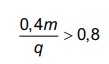
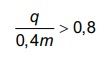
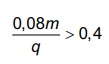
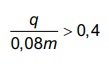

 , sendo
, sendo 



