Para determinadas pessoas que possuem dieta diferenciada ou querem
perder peso, existe uma grande variedade de alimentos indicados nessas
categorias, como produtos light e/ou diet.
Considerando-se que um alimento light contém, no máximo, um terço das
calorias da sua versão normal, ou contém menos da metade da quantidade
da gordura contida em sua versão normal, tem-se que se certo alimento
contém 84 calorias e 7,0g de gordura, então a sua versão light contém
Para determinadas pessoas que possuem dieta diferenciada ou querem perder peso, existe uma grande variedade de alimentos indicados nessas categorias, como produtos light e/ou diet.
Considerando-se que um alimento light contém, no máximo, um terço das calorias da sua versão normal, ou contém menos da metade da quantidade da gordura contida em sua versão normal, tem-se que se certo alimento contém 84 calorias e 7,0g de gordura, então a sua versão light contém






 = 4m e
= 4m e  = 3m, a razão
= 3m, a razão 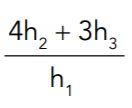 é igual a:
é igual a:
