Questõessobre Razão, Proporção e Números Proporcionais
A diferença de um número x pela razão
do número 60 por x é igual a - 7. Se x > 0, então o x2
vale:
Dados os triângulos nos gráficos das figuras 1 e 2
abaixo, consideremos os sólidos de volumes V1
e
V2
obtidos pela rotação completa dos triângulos das
figuras 1 e 2, respectivamente, em torno do eixo y.

A razão entre os volumes V1
e V2
é igual a
Dados os triângulos nos gráficos das figuras 1 e 2 abaixo, consideremos os sólidos de volumes V1 e V2 obtidos pela rotação completa dos triângulos das figuras 1 e 2, respectivamente, em torno do eixo y.

A razão entre os volumes V1
e V2
é igual a
O lixo produzido nas residências de todo o Brasil é
recolhido diariamente e transportado para diferentes
destinos. Na cidade de Porto Alegre, o lixo orgânico é
acomodado em caminhões que levam resíduos com
uma densidade média de 250 kg/m3
até o município
de Minas do Leão, a aproximadamente 100 km da
capital do RS. Em Minas do Leão, há um aterro
sanitário e uma central de tratamento de resíduos,
com capacidade estimada para receber 23 milhões
de toneladas de resíduos e com operação prevista
para os próximos vinte e três anos.
Com base nessas informações, se o lixo orgânico
produzido pelo município de Porto Alegre fosse
acomodado nos caminhões com uma densidade
_________ do que a atual, a massa de resíduos
transportada por viagem iria _________, e o custo
por tonelada transportada iria _________.
O lixo produzido nas residências de todo o Brasil é recolhido diariamente e transportado para diferentes destinos. Na cidade de Porto Alegre, o lixo orgânico é acomodado em caminhões que levam resíduos com uma densidade média de 250 kg/m3 até o município de Minas do Leão, a aproximadamente 100 km da capital do RS. Em Minas do Leão, há um aterro sanitário e uma central de tratamento de resíduos, com capacidade estimada para receber 23 milhões de toneladas de resíduos e com operação prevista para os próximos vinte e três anos.
Com base nessas informações, se o lixo orgânico produzido pelo município de Porto Alegre fosse acomodado nos caminhões com uma densidade _________ do que a atual, a massa de resíduos transportada por viagem iria _________, e o custo por tonelada transportada iria _________.
Um pai deseja dividir R$ 800,00 com seus dois
filhos de 10 anos e de 15 anos, em quantias
diretamente proporcionais às suas idades.
Quanto recebem, respectivamente, o filho mais
novo e o filho mais velho ?
Na Matemática, algumas razões são conhecidas e
encontradas na natureza, empregadas nas artes e na arquitetura, como o número 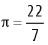 , aproximadamente, e
, aproximadamente, e 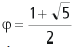 , conhecido como o número de ouro. O valor
de
, conhecido como o número de ouro. O valor
de 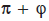 é, aproximadamente, de:
é, aproximadamente, de:
Na Matemática, algumas razões são conhecidas e
encontradas na natureza, empregadas nas artes e na arquitetura, como o número 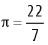 , aproximadamente, e
, aproximadamente, e 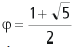 , conhecido como o número de ouro. O valor
de
, conhecido como o número de ouro. O valor
de 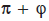 é, aproximadamente, de:
é, aproximadamente, de:
A tabela seguinte fornece o número de peças defeituosas
por peças confeccionadas em uma determinada fábrica.

A razão entre a média das peças confeccionadas e a média das peças defeituosas é igual a:


Uma pessoa ganhou uma lata de biscoitos de forma cilíndrica e, ao abri-la, constatou
que os biscoitos vinham acondicionados em quatro caixas retangulares de mesmo
tamanho, como ilustrado na figura 1.
Na figura 2, tem-se a representação de uma seção transversal da lata cuja medida do
raio forma, com as dimensões da base de cada caixa, uma progressão aritmética de razão 2.
Considerando-se que a lata e as caixas têm a mesma altura, pode-se afirmar que a razão
entre as capacidades da lata e das quatro caixas é igual a

A razão dos lados adjacentes de uma folha
retangular é 2/5. “Colando” os dois lados
maiores da folha, obtemos o cilindro C1 e
“colando” os dois lados menores da folha,
obtemos o cilindro C2
. A razão entre os
volumes de C1 e C2
é
Em uma festa de bodas de prata de um casal, compareceram
n
pessoas. Em um dado instante, 40 mulheres se retiraram e
restaram convidados na razão 2 homens para cada mulher. Um
pouco mais tarde, 30 homens se retiraram e restaram,
posteriormente, convidados na razão 3 mulheres para cada
homem. O número
n
de pessoas presentes, inicialmente, na
festa era igual a:
Um marido apaixonado resolveu prestar uma homenagem à sua esposa, construindo um jardim em
forma de coração por meio de um quadrado e dois semicírculos, conforme a fi gura. Para construí-lo, ele
usou mudas de flores vermelhas na razão de 200 mudas por metro quadrado. Assim, o total de mudas
utilizadas na montagem de tal jardim foi de (Considere π=3).

Um marido apaixonado resolveu prestar uma homenagem à sua esposa, construindo um jardim em
forma de coração por meio de um quadrado e dois semicírculos, conforme a fi gura. Para construí-lo, ele
usou mudas de flores vermelhas na razão de 200 mudas por metro quadrado. Assim, o total de mudas
utilizadas na montagem de tal jardim foi de (Considere π=3).

Um produto foi comprado em 2 parcelas, a primeira à vista e a segunda após 3 meses, de maneira que,
sobre o saldo devedor, incidiram juros simples de 2% ao mês. Se o valor das 2 parcelas foi o mesmo,
em relação ao preço do produto à vista, cada parcela corresponde à
No início de determinado dia, um laboratório dispõe de várias
seringas descartáveis para uso. Ao término desse dia, a razão entre o número de seringas não utilizadas e o de utilizadas era 2/9.Se 15 das seringas utilizadas não tivessem sido
usadas nesse dia, a razão entre o número de seringas não
utilizadas e o de utilizadas teria sido 1/3. O número de seringas
descartáveis disponíveis no início desse dia era
O Tangram é um quebra-cabeça chinês que contém sete peças: um quadrado, um paralelogramo
e cinco triângulos retângulos isósceles. Na figura, o quadrado ABCD é formado com as peças
de um Tangram.

Observe os seguintes componentes da figura:
• NP – lado do quadrado;
• AM – lado do paralelogramo;
• CDR e ADR – triângulos congruentes, bem como CNP e RST.
A razão entre a área do trapézio AMNP e a área do quadrado ABCD equivale a:

UTILIZE AS INFORMAÇÕES A SEGUIR PARA RESPONDER A QUESTÃO.
Casos de febre amarela desde o início de 2017:
• confirmados → 779;
• suspeitos → 435.
Mortes entre os casos confirmados: 262.
Suponha que todos os casos suspeitos tenham sido comprovados, e que a razão entre o número
de mortes e o de casos confirmados permaneça a mesma.
Nesse caso, com as novas comprovações da doença, o número total de mortos por febre amarela
estaria mais próximo de:
Três teses sobre o avanço da febre amarela

NATHALIA PASSARINHO
Adaptado de bbc.com, 06/02/2018.
Observando os dados exibidos na reportagem acima, é correto afirmar
que:

Se no cubo da figura,  , então a razão
entre o volume e a área total desse cubo é
, então a razão
entre o volume e a área total desse cubo é

Se no cubo da figura,  , então a razão
entre o volume e a área total desse cubo é
, então a razão
entre o volume e a área total desse cubo é
Em uma palestra, um cientista ilustrou comparativamente o
tamanho dos planetas do sistema solar com auxílio da foto
a seguir.

No entanto, o cientista disse que essa foto dificulta a percepção correta da diferença de tamanho entre os planetas. Para
ilustrar o que dizia, ele pediu para a plateia considerar que todos os planetas são esféricos e que o tamanho do raio do planeta Júpiter é 11 vezes o tamanho do raio do planeta Terra.
Em seguida, lançou a seguinte pergunta: se associarmos o
planeta Terra a uma bola de futebol, o planeta Júpiter deverá
ser associado, aproximadamente, a quantas dessas bolas?
A resposta correta para a pergunta do palestrante é
Em uma palestra, um cientista ilustrou comparativamente o tamanho dos planetas do sistema solar com auxílio da foto a seguir.

No entanto, o cientista disse que essa foto dificulta a percepção correta da diferença de tamanho entre os planetas. Para ilustrar o que dizia, ele pediu para a plateia considerar que todos os planetas são esféricos e que o tamanho do raio do planeta Júpiter é 11 vezes o tamanho do raio do planeta Terra. Em seguida, lançou a seguinte pergunta: se associarmos o planeta Terra a uma bola de futebol, o planeta Júpiter deverá ser associado, aproximadamente, a quantas dessas bolas?
A resposta correta para a pergunta do palestrante é
As figuras a seguir mostram dois pacotes de café em pó que têm a forma de paralelepípedos
retângulos semelhantes.

Se o volume do pacote maior é o dobro do volume do menor, a razão entre a medida da área
total do maior pacote e a do menor é igual a:
As figuras a seguir mostram dois pacotes de café em pó que têm a forma de paralelepípedos retângulos semelhantes.

Se o volume do pacote maior é o dobro do volume do menor, a razão entre a medida da área total do maior pacote e a do menor é igual a:



