Considere a figura abaixo, onde um quadrado está
representado no primeiro quadrante do plano xy.
Para que uma reta da forma y = x + m não intercepte
qualquer ponto do quadrado, devemos ter

Considere a figura abaixo, onde um quadrado está representado no primeiro quadrante do plano xy. Para que uma reta da forma y = x + m não intercepte qualquer ponto do quadrado, devemos ter








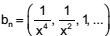 onde n ≥ 1. Se a
onde n ≥ 1. Se a