Questõesde PUC - PR sobre Matemática
Em uma divisão, a soma do resto r, divisor d e dividendo D é 178. Se o quociente é 7 e o resto é o maior valor possível,
qual o valor da soma do dividendo com o resto?
Assinale a alternativa CORRETA.
Leia o texto a seguir.
A lenda do jogo de xadrez
A lenda conta que um rei hindu teve o conhecimento de um jogo que é composto de 32 peças, no qual o objetivo é capturar a peça mais importante, o rei do adversário, através de um sábio brâmane, chamado Sessa, que queria lhe tirar da depressão que o abatera depois da morte de seu filho. Após algumas partidas jogadas, a satisfação do rei foi tamanha que deu o direito ao brâmane de escolher o que ele quisesse no reino como premiação. Sessa fez então um pedido inusitado: um tabuleiro com grãos de trigo que,na primeira casa tivesse um grão, na segunda, dois, na terceira, quatro, dobrando sempre até a casa de número 64 e somando todos os valores encontrados ao final. O rei mandou então os algebristas de seu reino fazerem os cálculos. A respeito dessa situação, julgue os itens a seguir.
I. A sequência proposta por Sessa: 1 grão na primeira casa, na segunda dois, na terceira quatro etc. É uma progressão aritmética de razão 2.
II. A sequência proposta por Sessa: 1 grão na primeira casa, na segunda dois, na terceira quatro etc. É uma progressão geométrica de razão 2.
III. A soma dos termos da progressão vale 2⁵⁴.
IV. A soma dos termos da progressão vale 2080.
Clarice e suas colegas de Engenharia resolveram organizar uma festa junina para arrecadar fundos para
a formatura. Com esse intuito, montaram três quiosques, nos quais eram vendidos pipoca, cachorro
quente e quentão. Ao término da festa, foi feito o levantamento das vendas nos três quiosques:
No primeiro, foram vendidos 10 sacos de pipoca, 20 cachorros quentes e 10 copos de quentão.
No segundo, foram vendidos 50 sacos de pipoca, 40 cachorros quentes e 20 copos de quentão.
No terceiro, foram vendidos 20 sacos de pipoca, 10 cachorros quentes e 30 copos de quentão.
Os três quiosques lucraram R$ 150,00, R$ 450,00 e R$ 250,00 respectivamente.
Assinale a alternativa que apresenta o preço de cada saco de pipoca, cachorro quente e copo de quentão,
respectivamente.
Clarice e suas colegas de Engenharia resolveram organizar uma festa junina para arrecadar fundos para a formatura. Com esse intuito, montaram três quiosques, nos quais eram vendidos pipoca, cachorro quente e quentão. Ao término da festa, foi feito o levantamento das vendas nos três quiosques:
No primeiro, foram vendidos 10 sacos de pipoca, 20 cachorros quentes e 10 copos de quentão.
No segundo, foram vendidos 50 sacos de pipoca, 40 cachorros quentes e 20 copos de quentão.
No terceiro, foram vendidos 20 sacos de pipoca, 10 cachorros quentes e 30 copos de quentão.
Os três quiosques lucraram R$ 150,00, R$ 450,00 e R$ 250,00 respectivamente.
Assinale a alternativa que apresenta o preço de cada saco de pipoca, cachorro quente e copo de quentão,
respectivamente.
As leis governamentais dos Estados Unidos exigem que, antes que o querosene possa ser usado como combustível de jatos, deve haver a remoção dos poluentes do querosene com uso de argila. A argila fica no interior de um tubo e cada metro do tubo remove 20% dos poluentes que entram nele. Seja P₀ a quantidade
inicial de poluentes e P = f(n) a quantidade de poluentes que ainda permanecem após n metros da
tubulação, a função P = f(n) que melhor representa a quantidade de poluentes retidos no tubo é
P = P₀(0,8)n
P = P₀(0,2)n
Um topógrafo deseja medir a distância x de um ponto Q na margem de um rio até um ponto inacessível P
na outra margem, conforme a figura. Sabendo-se que ele visualiza o ponto P segundo um ângulo β e, em
seguida, ele se desloca uma distância b até o ponto R e observa o ponto P segundo o ângulo θ, a expressão
que calcula a distância x é







Em duas urnas, há 5 fichas em cada. Em ambas as urnas, as fichas estão numeradas de 1 a 5. Qual a
probabilidade de, ao se retirar duas fichas, uma de cada urna, a soma dos números ser um número primo
ou quadrado perfeito?
16/25
14/25
13/25
17/55
15/25
Um medicamento que dilata os vasos e artérias do corpo humano é ministrado e aumenta o diâmetro em
20% de determinada artéria. Considerando que a artéria se assemelha a um cilindro circular reto, o fluxo
sanguíneo nessa artéria aumenta em
Considere uma caixa de leite na forma de um paralelepípedo de base quadrada, cujo volume é de 1 litro.O custo de fabricação da tampa e da base da caixa é de R$ 4,00 por cm², e o das faces laterais é de R$2,00 por cm²; considere desprezível o custo da tampinha de plástico. Determine uma função C(x) queexpresse o custo de fabricação da caixa em função da aresta da base que vale x. 




As soluções (valores de z) na equação zn = K, sendo 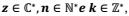 são pontos de uma
circunferência. Calcule a área do setor circular
formado nessa circunferência, tal que as
extremidades do arco que forma o setor sejam duas
soluções consecutivas da equação.
são pontos de uma
circunferência. Calcule a área do setor circular
formado nessa circunferência, tal que as
extremidades do arco que forma o setor sejam duas
soluções consecutivas da equação.
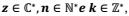 são pontos de uma
circunferência. Calcule a área do setor circular
formado nessa circunferência, tal que as
extremidades do arco que forma o setor sejam duas
soluções consecutivas da equação.
são pontos de uma
circunferência. Calcule a área do setor circular
formado nessa circunferência, tal que as
extremidades do arco que forma o setor sejam duas
soluções consecutivas da equação.
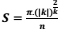



Determine a equação da reta que passa pela origem
do sistema cartesiano e é tangente à parábola de
equação x2 − y + 2 = 0 num ponto do 2º quadrante.
x + √2 y = 0
4
Com a aproximação da Copa do Mundo de futebol
uma empresa resolveu fazer uma promoção e para
isso pretende adquirir 10 ingressos para alguns dos
jogos da Copa e distribuí-los para 5 funcionários.
Suponha que a tabela abaixo represente os possíveis
ingressos adquiridos:
JOGOS QUANTIDADE DE
INGRESSOS
A 3
B 2
C 1
D 1
E 1
F 1
G 1
Para sortear os cinco ingressos entre os funcionários,
a empresa estabeleceu o seguinte critério:
• Dois ingressos deverão ser para o mesmo
jogo.
• Três ingressos deverão ser para jogos
diferentes entre si e também diferentes dos
dois outros jogos.
De acordo com esses critérios, o número máximo de
conjuntos distintos entre si que podem ser formados é
igual a:
Com a aproximação da Copa do Mundo de futebol uma empresa resolveu fazer uma promoção e para isso pretende adquirir 10 ingressos para alguns dos jogos da Copa e distribuí-los para 5 funcionários. Suponha que a tabela abaixo represente os possíveis ingressos adquiridos:
JOGOS QUANTIDADE DE
INGRESSOS
A 3
B 2
C 1
D 1
E 1
F 1
G 1
Para sortear os cinco ingressos entre os funcionários, a empresa estabeleceu o seguinte critério:
• Dois ingressos deverão ser para o mesmo jogo.
• Três ingressos deverão ser para jogos diferentes entre si e também diferentes dos dois outros jogos.
De acordo com esses critérios, o número máximo de
conjuntos distintos entre si que podem ser formados é
igual a:
Sabe-se que a representação gráfica de uma função
polinomial do 1º grau é uma reta. Se considerarmos
as funções f(x) = 5/12 x − 21/6 , g(x) = − 5/16 x +
7/2 e h(x) = − 1/4 x + m/20 com seus respectivos gráficos num mesmo plano cartesiano, qual o valor de m para
que os três gráficos sejam concorrentes num único
ponto?
Se θ e φ são os ângulos agudos de um triângulo retângulo, calcule o valor da expressão 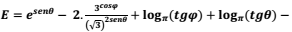
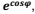 sabendo que π é uma constante de valor aproximado de 3,1417 e e é uma constante de valor aproximado de 2,71.
sabendo que π é uma constante de valor aproximado de 3,1417 e e é uma constante de valor aproximado de 2,71.
Se θ e φ são os ângulos agudos de um triângulo retângulo, calcule o valor da expressão 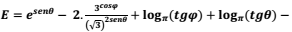
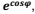 sabendo que π é uma constante de valor aproximado de 3,1417 e e é uma constante de valor aproximado de 2,71.
sabendo que π é uma constante de valor aproximado de 3,1417 e e é uma constante de valor aproximado de 2,71.
Um cilindro reto de altura √6/ 3 cm está inscrito numa
pirâmide reta triangular regular e tem sua base em
uma das faces da pirâmide. Se as arestas lateral e da
base da pirâmide medem 3 cm, o volume do cilindro,
em cm3
, é igual a:
π√3
6
π√6
9
π√6
6
π√3
4
π
3
O “PODER” DE UMA FOFOCA
Um senhor, há muito tempo, tanto falou que seu
vizinho era ladrão, que o rapaz acabou preso! Dias
depois, descobriram que era inocente.
O rapaz foi solto e processou o homem.
No tribunal, o velho diz ao juiz:
- Comentários não causam tanto mal.
E o juiz responde:
- Escreva os comentários num papel, depois pique e
jogue os pedaços no caminho de casa. Amanhã, volte
para ouvir a sentença.
O senhor obedeceu e voltou no dia seguinte.
- Antes da sentença, terá que catar os pedaços de
papel que espalhou ontem - disse o juiz.
Responde o velho:
- Não posso fazer isso. O vento deve tê-los espalhado
já não sei onde estão.
Responde o juiz:
- Da mesma maneira, um simples comentário pode
destruir a honra de um homem, a ponto de não
podermos consertar o mal. Se não se pode falar bem
de uma pessoa, é melhor que não se diga nada.
O fofoqueiro da ilustração precisa, de uma forma
discreta, denegrir a imagem do seu concorrente
dentro do reduto de clientes nos níveis nacional e
internacional. É necessário que a fofoca atinja um
grupo de trezentas mil pessoas e, para ser discreto,
num período de 5 minutos, contou essa fofoca para
duas pessoas instruindo que cada uma dessas duas
pessoas levaria cinco minutos para contar a fofoca a
outras duas novas pessoas. Sucessivamente isso foi
feito. Considerando que, para todos se protegerem,
uma pessoa conta a fofoca apenas uma vez para
outras duas pessoas, em quanto tempo todo o reduto
de clientes saberá da fofoca? (Considerar 100,5 ≅
3 e 100,3 ≅ 2)
O “PODER” DE UMA FOFOCA
Um senhor, há muito tempo, tanto falou que seu
vizinho era ladrão, que o rapaz acabou preso! Dias
depois, descobriram que era inocente.
O rapaz foi solto e processou o homem.
No tribunal, o velho diz ao juiz:
- Comentários não causam tanto mal.
E o juiz responde:
- Escreva os comentários num papel, depois pique e
jogue os pedaços no caminho de casa. Amanhã, volte
para ouvir a sentença.
O senhor obedeceu e voltou no dia seguinte.
- Antes da sentença, terá que catar os pedaços de
papel que espalhou ontem - disse o juiz.
Responde o velho:
- Não posso fazer isso. O vento deve tê-los espalhado
já não sei onde estão.
Responde o juiz:
- Da mesma maneira, um simples comentário pode
destruir a honra de um homem, a ponto de não
podermos consertar o mal. Se não se pode falar bem
de uma pessoa, é melhor que não se diga nada.
O fofoqueiro da ilustração precisa, de uma forma
discreta, denegrir a imagem do seu concorrente
dentro do reduto de clientes nos níveis nacional e
internacional. É necessário que a fofoca atinja um
grupo de trezentas mil pessoas e, para ser discreto,
num período de 5 minutos, contou essa fofoca para
duas pessoas instruindo que cada uma dessas duas
pessoas levaria cinco minutos para contar a fofoca a
outras duas novas pessoas. Sucessivamente isso foi
feito. Considerando que, para todos se protegerem,
uma pessoa conta a fofoca apenas uma vez para
outras duas pessoas, em quanto tempo todo o reduto
de clientes saberá da fofoca? (Considerar 100,5 ≅
3 e 100,3 ≅ 2)
Numa certa cidade, a Companhia Elétrica responsável
pelo fornecimento e supervisão da energia na cidade
tem as seguintes regras de cobrança mensal dos seus
usuários: para os primeiros 200 kWh consumidos, o
preço de cada kWh é R$ 0,24; para os 300 kWh
seguintes consumidos, o preço de cada kWh é R$
0,36. O preço de cada kWh consumido acima de 500
kWh é R$ 0,72.
Dado a esse contexto, analise as afirmações abaixo e
marque a alternativa CORRETA.
I. Se P é o valor em reais a ser pago pelo
consumidor após um consumo de n kWh, e se n
for igual a 250, P será igual a 90.
II. Se P é o valor em reais a ser pago pelo
consumidor após um consumo de n kWh, pode-se
dizer que P(n)= 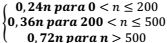
Se 200 < n ≤ 500, o valor máximo que poderá
ser pago pelo consumidor será igual a R$
156,00
É correto o que se afirma APENAS em:
Numa certa cidade, a Companhia Elétrica responsável pelo fornecimento e supervisão da energia na cidade tem as seguintes regras de cobrança mensal dos seus usuários: para os primeiros 200 kWh consumidos, o preço de cada kWh é R$ 0,24; para os 300 kWh seguintes consumidos, o preço de cada kWh é R$ 0,36. O preço de cada kWh consumido acima de 500 kWh é R$ 0,72.
Dado a esse contexto, analise as afirmações abaixo e marque a alternativa CORRETA.
I. Se P é o valor em reais a ser pago pelo consumidor após um consumo de n kWh, e se n for igual a 250, P será igual a 90.
II. Se P é o valor em reais a ser pago pelo
consumidor após um consumo de n kWh, pode-se
dizer que P(n)= 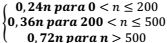
Se 200 < n ≤ 500, o valor máximo que poderá ser pago pelo consumidor será igual a R$ 156,00
É correto o que se afirma APENAS em:
. A espiral abaixo representa as ruas AB, BC, CD, DE e
EF de uma cidade.
Uma pessoa se encontra no ponto A e precisa chegar
no ponto F fazendo a seguinte rota:

Sabe-se que, nessa sequência, a medida de cada rua
corresponde a 75% da medida da rua anterior.

Se 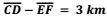 , então, a rua
, então, a rua 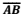 , em
quilômetros, mede:
, em
quilômetros, mede:
. A espiral abaixo representa as ruas AB, BC, CD, DE e EF de uma cidade.
Uma pessoa se encontra no ponto A e precisa chegar no ponto F fazendo a seguinte rota:

Sabe-se que, nessa sequência, a medida de cada rua corresponde a 75% da medida da rua anterior.

Se 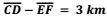 , então, a rua
, então, a rua 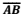 , em
quilômetros, mede:
, em
quilômetros, mede:
Um consumidor, ao adquirir um automóvel, assumiu um empréstimo no valor total de R$ 42.000,00 (já somados juros e encargos). Esse valor foi pago em 20 parcelas, formando uma progressão aritmética decrescente. Dado que na segunda prestação foi pago o valor de R$ 3.800,00, a razão desta progressão aritmética é:
Considere as funções f(x) = x2 + 1 e g(x) = – x+3. A distância entre o ponto A (4, 6) e o ponto de interseção das funções f(x) e g(x) no primeiro quadrante, em u. c. (unidades de comprimento), é:
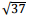 u. c.
u. c.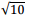 u. c.
u. c.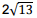 u. c.
u. c.