Questõessobre Progressões
Numa progressão aritmética de razão r e primeiro termo 3, a soma dos primeiros n termos é 3n2, logo, a razão
é:
Em uma progressão geométrica com 7 termos positivos, o primeiro ter-
mo é igual a √18 e o sétimo termo é igual a √2. Nessas condições, se
multiplicarmos o terceiro, o quarto e o quinto termos, obteremos como
produto:
Nos últimos anos, milhares de pessoas
chegaram à Europa depois de atravessarem o Mar Mediterâneo. Os números
foram 3300 em janeiro e 45 375 em dezembro
de 2014.
Fonte: Disponível em: <www.gazetadopovo.com.br/mundo/so-nesteano-mais-de-500-mil-imigrantes-cruzam-o-mediterraneo8assnmxyrzxtewt4zoaeu5o1o>. Acesso em: 28 nov. 2016. (Adaptado)
O número de chegadas em maio e o total de chegadas em 2014 foram, respectivamente, de:
Os números reais n - 6, n - 4, 2n - 11 são os três
primeiros termos consecutivos de uma progressão
geométrica crescente. O quarto termo dessa P.G. é
Se os arcos α, β e γ, nessa ordem, formam uma progressão aritmética, então a expressão
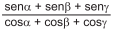 é equivalente a
é equivalente a
Se os arcos α, β e γ, nessa ordem, formam uma progressão aritmética, então a expressão
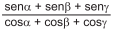 é equivalente a
é equivalente a
Em uma progressão aritmética (PA), a soma do terceiro
com o sexto termo é 31, e a soma do quarto termo
com o sétimo termo é 37. Logo, a soma do segundo
com o oitavo termo dessa PA vale
Em uma progressão aritmética, o sexto termo vale 6 e
o décimo terceiro vale –15. Então, o vigésimo termo
dessa P.A. vale
Se a soma dos n primeiros termos de uma progressão aritmética é dada pela expressão  ,
então a soma do segundo com o décimo termo dessa progressão é
,
então a soma do segundo com o décimo termo dessa progressão é
Se a soma dos n primeiros termos de uma progressão aritmética é dada pela expressão  ,
então a soma do segundo com o décimo termo dessa progressão é
,
então a soma do segundo com o décimo termo dessa progressão é
Os lados de um triângulo retângulo estão em P.A. de
razão 3. Então, os valores dos lados são
Em uma progressão geométrica o primeiro termo é 3 e
o terceiro é 12; então, a soma dos 8 primeiros termos é:
Uma locadora de filmes possui a seguinte regra para cobrança de multa para devoluções com atraso: para cada item locado, cobra R$ 2,50 para o primeiro dia de atraso e, a partir do segundo dia, R$ 0,50 a mais para cada dia de atraso. O cliente A está com uma grande quantidade de itens em atraso e, no décimo quinto dia, faz o seguinte acordo com a locadora: paga a metade da multa e, a cada 5 dias, pagará a metade do montante da multa; e o valor de R$ 0,50 por dia de atraso continuará sendo cobrado. Baseado nessas informações, assinale a alternativa correta.
Para cada m = 0,1,2,…, o termo 5m fornece o dia de
cada pagamento do cliente A, a partir do 15° dia de
atraso. A fórmula 19/2m+1 + 5/2(1 - 1/2m) fornece o valor em reais a ser pago para cada filme em atraso do
cliente A.
A sequência Q(0), Q(1), Q(2),…,Q(n)…, em que n ∈ ℕ, é uma progressão aritmética.
Se P =100 , k = 0,02 e x0 = 50 , então os valores
xn , n=1,2,3,... formam uma progressão geométrica.
Assinale a alternativa correta.
Se a e b são o segundo e o quarto termos,
respectivamente, de uma progressão
geométrica, em que o primeiro termo é 1 e a
razão é 2, então h2 = 70.
MATEMÁTICA - Formulário
Dado um triângulo ABC, retângulo em A, sejam h, a
e b as medidas, em unidades de comprimento, dos
lados BC, AB e AC, respectivamente. Em relação ao
exposto, assinale o que for correto.
Se a sequência (a, b, h) é uma progressão
aritmética de razão 2, a área da região
triangular ABC é 24 unidades de área.
MATEMÁTICA - Formulário
Dado um triângulo ABC, retângulo em A, sejam h, a
e b as medidas, em unidades de comprimento, dos
lados BC, AB e AC, respectivamente. Em relação ao
exposto, assinale o que for correto.
Se z ∈ ℤ e  , em que n ∈ ℕ e 1 ≤ n ≤ 10, então z é um divisor de 20.
, em que n ∈ ℕ e 1 ≤ n ≤ 10, então z é um divisor de 20.
Se z ∈ ℤ e , em que n ∈ ℕ e 1 ≤ n ≤ 10, então z é um divisor de 20.
MATEMÁTICA - Formulário
A respeito dos conjuntos numéricos e de suas
propriedades, assinale o que for correto.
As prestações de um financiamento imobiliário constituem uma progressão aritmética na ordem
em que são pagas. Sabendo que a 15ª prestação é R$ 3 690,00 e a 81ª prestação é R$ 2 700,00, o
valor da 1ª prestação é
As prestações de um financiamento imobiliário constituem uma progressão aritmética na ordem em que são pagas. Sabendo que a 15ª prestação é R$ 3 690,00 e a 81ª prestação é R$ 2 700,00, o valor da 1ª prestação é
A razão entre o elemento (a61) e (a51) é igual à
razão entre o elemento (a32) e (a72).
A questão se refere ao quadro a seguir.
Animal “Peso” médio do corpo (g) Consumo de oxigênio (g/h)
Camundongo 25 1.580
Rato 226 872
Coelho 2.200 466
Cão 11.700 318
Ser humano 70.000 202
Cavalo 700.000 106
Elefante 3.800.000 67
Fonte: PAULINO, W.R.. Biologia. Série Novo Ensino Médio. São Paulo: Ática, 2004, p. 262.
Considere a matriz M = (aij), de acordo com a
ordem dada no quadro, em que, nas linhas i, estão
os animais; na primeira e na segunda colunas da
matriz, estão, respectivamente, o “peso” médio do
corpo, em gramas, e o consumo de oxigênio, em
gramas por hora, e assinale o que for correto.
A sequência SA(t0),SA(t1),SA(t2),..., em que SA(t) denota a posição de A no instante t , em metros, é uma
progressão geométrica.

Dois pontos materiais, A e B, desenvolvem movimentos retilíneos uniformes ao longo da mesma reta orientada com velocidade positiva. A velocidade vB de B é o dobro da velocidade vA de A (em metros por segundo). No instante t = 0 s, B ocupa a posição 0 m e A ocupa a posição d metros, sendo d > 0. Definimos a sequência t0,t1,...,tn,..., em que t0 = 0 e tn+1 é o instante, em segundos, de modo que a posição de B no instante tn+1 é a posição de A no instante tn, para cada n ∈ ℕ. Definimos, ainda, para todo n natural positivo, an como sendo an = tn - tn -1. Considerando esses dados, assinale a alternativa correta.