Questõessobre Pontos e Retas
Assinale a alternativa que indica a distância, no plano cartesiano, entre os pontos de coordenadas (-3, 2) e o centro da
circunferência definida pela equação x² + y² - 4x + 10y + 20 = 0.
Assinale a alternativa que indica o valor da incógnita “a”, de forma que a reta que passa pelos pontos P1(2, 3) e P2(5, a)
forme um ângulo de 45 graus com o eixo X no plano cartesiano.
Em um plano cartesiano estão alocados os pontos A(4, 1), B(1, 3), C(0, 1) e D(2, 0).
Assinale a alternativa que contempla as coordenadas do ponto de intersecção entre a reta G, que passa pelos pontos A e B e
a reta H, que passa pelos pontos C e D.
Descreva essas informações, julgue o item a seguir.
Se os pontos O, A e D primeiros colineares, e se D para o ponto médio do segmento AE, então como coordenadas do ponto E serão (100, 100).
Descreva essas informações, julgue o item a seguir.
Se os pontos O, A e D primeiros colineares, e se D para o ponto médio do segmento AE, então como coordenadas do ponto E serão (100, 100).

Descreva essas informações, julgue o item a seguir.
A partir da identificação dos pontos P = (x, y) do plano cartesiano com números globais da forma z = x + iy, é correto afirmar que o quadrado do número complexo relativo ao ponto A será igual a 400 (1 + i).
Descreva essas informações, julgue o item a seguir.
A partir da identificação dos pontos P = (x, y) do plano cartesiano com números globais da forma z = x + iy, é correto afirmar que o quadrado do número complexo relativo ao ponto A será igual a 400 (1 + i).

Nesta figura, o ponto B pertence à bissetriz do primeiro quadrante.

Sabendo-se que o ponto A é dado por A= (6,0) e que a área do triângulo OAB é igual a 15, a equação da reta que passa por A e B é dada por:
Nesta figura, o ponto B pertence à bissetriz do primeiro quadrante.

Sabendo-se que o ponto A é dado por A= (6,0) e que a área do triângulo OAB é igual a 15, a equação da reta que passa por A e B é dada por:
Duas circunferências com raios 1 e 2 têm centros no
primeiro quadrante do plano cartesiano e ambas
tangenciam os dois eixos coordenados. Essas circunferências
se interceptam em dois pontos distintos de coordenadas
(x1, y1) e (x2, y2).
O valor de ( x1 + y1)2 + (x2 + y2)2 é igual a
Duas circunferências com raios 1 e 2 têm centros no primeiro quadrante do plano cartesiano e ambas tangenciam os dois eixos coordenados. Essas circunferências se interceptam em dois pontos distintos de coordenadas (x1, y1) e (x2, y2).
O valor de ( x1 + y1)2 + (x2 + y2)2 é igual a
Desenhando sobre um mesmo sistema de eixos
cartesianos os gráficos de y = x2 + 1 e de x2 + y2 = 4 , quantos pontos em comum a ambos
existirão?
Qual é a razão entre a medida da área e do comprimento da circunferência que, no plano
cartesiano, passa pelos pontos A (-4, 1), B (-1, - 2) e C (2, 1)?
No plano, a distância do ponto P ao centro O da circunferência cuja medida do raio é 2 cm, é igual a 4 cm. Traçam-se, pelo ponto P, duas retas que tangenciam a circunferência nos pontos M e N determinando o quadrilátero MPNO. A medida, em cm2, da área da região interior ao quadrilátero e exterior à circunferência é
Na fi gura a seguir, ABCD é um retângulo e o
ponto E é a interseção dos segmentos 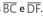 .
Se BE = 2; CE, EF = 2; DE, AB = 4 cm e
AD = 9 cm, qual das medidas a seguir
mais se aproxima de CF?
.
Se BE = 2; CE, EF = 2; DE, AB = 4 cm e
AD = 9 cm, qual das medidas a seguir
mais se aproxima de CF?

Na fi gura a seguir, ABCD é um retângulo e o
ponto E é a interseção dos segmentos 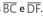 .
Se BE = 2; CE, EF = 2; DE, AB = 4 cm e
AD = 9 cm, qual das medidas a seguir
mais se aproxima de CF?
.
Se BE = 2; CE, EF = 2; DE, AB = 4 cm e
AD = 9 cm, qual das medidas a seguir
mais se aproxima de CF?

No plano cartesiano ortogonal, o triângulo de vértices A(2, 3),
B(6,1) e C(5, 5) foi intersectado no ponto P por uma reta que
passa por C e é perpendicular a AB, conforme indica a figura.

Na situação descrita, a ordenada y do ponto P é igual a

A figura abaixo representa um retângulo
formado pela justaposição de três quadrados.

Assim, as medidas dos segmentos AB, BC, CD, EF,
FG, GH, AE, BF, CG e DH são iguais. Nestas
condições, podemos afirmar corretamente que a
soma das medidas, em graus, dos ângulos CÊH e
DÊH é igual a
A figura abaixo representa um retângulo formado pela justaposição de três quadrados.

Assim, as medidas dos segmentos AB, BC, CD, EF,
FG, GH, AE, BF, CG e DH são iguais. Nestas
condições, podemos afirmar corretamente que a
soma das medidas, em graus, dos ângulos CÊH e
DÊH é igual a
Considere os pontos A (0, 0), B (4, 0) e C (4, 3) do plano cartesiano. Ao
girarmos a região triangular ABC em torno do eixo das abscissas,
obteremos um sólido de revolução cujo volume é:
No plano cartesiano, os pontos A (–2, –1), B (1, 3) e C (5, –1) são, nessa
ordem, vértices consecutivos de um paralelogramo. O quarto vértice
tem coordenadas cuja soma é:
Uma circunferência tem centro no 1º quadrante, tangencia os eixos
cartesianos e passa pelo ponto de coordenadas (1, 2).
Um possível valor de seu raio é:
Em uma alameda, plantamos 10 roseiras em linha reta.
A roseira R1 está no início da alameda. Sabe-se que a
distância entre R1 e R2
é de 1 metro, a distância entre R2
e R3
é de 2 metros. Em geral, a distância entre Rk
e Rk+1
é de k metros.
Quanto vale, em metros, a distância entre a primeira
roseira R1
e a última roseira R10?
O retângulo ABCD, com A = (0, 0), B sobre o semieixo x
positivo, D sobre o semieixo y positivo, conforme figura
abaixo, tem área 36, e a medida do lado AD é igual a 4.

Qual é a equação da reta BD?
