32b46b1c-0b
UECE 2021 - Matemática - Polinômios
Seja P(x)=x3+ px2+ qx – 2 onde p e q são
números reais tais que P(1+i)=0. Nestas condições,
em relação às raízes x1e x2 da equação
x2+qx–p=0, pode-se afirmar corretamente que a
soma 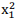 +
+ 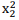 é igual a
é igual a
Seja P(x)=x3+ px2+ qx – 2 onde p e q são
números reais tais que P(1+i)=0. Nestas condições,
em relação às raízes x1e x2 da equação
x2+qx–p=0, pode-se afirmar corretamente que a
soma 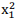 +
+ 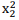 é igual a
é igual a
A
10.
B
5.
C
26.
D
17.