Questõessobre Polinômios

InícioTodas as questões
1
1
Foram encontradas 209 questões
90faa676-6e
INSPER 2018 - Matemática - Polinômios

O custo C de um produto em função da quantidade x fabricada desse produto é dado pelo polinômio C(x). Dividindo-se C(x) por x – 19, o resto será igual a 99, ao passo que a divisão de C(x) por x – 99 deixa resto 19. Se cálculos econômicos exigirem que se faça a divisão de C(x) pelo polinômio (x – 19) · (x – 99), o resto dessa divisão será o polinômio

A
20 – x.
B
118 – x.
C
80 – x.
D
20 + x.
E
80 + x.
332bac6d-58
UNESP 2018 - Matemática - Quadriláteros, Funções, Geometria Plana, Polinômios, Função de 2º Grau

Sendo x um número real maior que 2/3 , a área de um retângulo é dada pelo polinômio 3x2 + 19x –14. Se a base desse retângulo é dada pelo polinômio x + 7, o quadrado da diagonal do retângulo é expresso pelo polinômio

A
10x2 + 26x + 29.
B
10x2 + 53.
C
10x2 + 65.
D
4x2 + 2x + 53.
E
10x2 + 2x + 53.
e31596c4-38
UNICAMP 2017 - Matemática - Polinômios

Sejam p(x) e q(x) polinômios com coeficientes reais.Dividindo-se p(x) por q(x), obtêm-se quociente e resto iguais a x² + 1. Nessas condições, é correto afirmar que

A
o grau de p(x) é menor que 5.
B
o grau de q(x) é menor que 3.
C
p(x) tem raízes complexas.
D
q(x) tem raízes reais.
366c2523-42
FGV 2016 - Matemática - Polinômios

Um dos fatores do polinômio P(x) = x3 + 2x2 − 5x − 6 é (x + 3) . Outro fator desse polinômio é

A
(x + 8)
B
(x - 5)
C
(x + 4)
D
(x - 1)
E
(x + 1)
7a047918-31
UNESPAR 2016 - Matemática - Polinômios

Com relação aos polinômios P(x) = (x4 -1) . (x2 - 2) e Q(x) = x3 - x2 + x , é correto afirmar que:

I. O coeficiente de x6 em P(x) é zero.

II. x = 0 é raiz de Q(x).

III. x = 2 é raiz de P(x).

IV. O resto da divisão de P(x) por Q(x) é um polinômio de grau 2.

A
Todas as afirmações são verdadeiras;
B
Somente a IV é falsa;
C
Apenas II e IV são verdadeiras;
D
Somente I é verdadeira;
E
Apenas I e II são falsas.
6e507193-1d
UNICAMP 2016 - Matemática - Polinômios

Considere o polinômio p(x) = xn + xm + 1, em que n > m ≥ 1. Se o resto da divisão de p(x) por x + 1 é igual a 3, então

A
n é par e m é par.
B
n é ímpar e m é ímpar.
C
n é par e m é ímpar.
D
n é ímpar e m é par.
003e2cd7-e1
USP 2016 - Matemática - Álgebra, Equação do 2º Grau e Problemas do 2º Grau, Polinômios

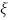O polinômio P(x) = x3 - 3x2 + 7x - 5 possui uma raiz complexa cuja parte imaginária é positiva. A parte real de 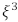é igual a

A
-11
B
-7
C
9
D
10
E
12
53118191-d6
PUC - RS 2016 - Matemática - Polinômios

Os polinômios p(x), q(x), f(x), h(x) em C , nessa ordem, estão com seus graus em progressão geométrica. Os graus de p(x) e h(x) são, respectivamente, 16 e 2. A soma do número de raízes de q(x) com o número de raízes de f(x) é

A
24
B
16
C
12
D
8
E
4
358b9acf-c0
FGV 2016 - Matemática - Polinômios

Um dos fatores do polinômio P(x) = x³ + 2x² - 5x - 6 é (x+3). Outrofator desse polinômio é

A
(x + 8)
B
(x - 5)
C
(x + 4)
D
(x - 1)
E
(x + 1)
4151f5f1-b2
UFU-MG 2016 - Matemática - Polinômios

Considere o polinômio de variável real p(x) = x3 - kx + 150, com k sendo um número natural fixo não nulo.
Se o número complexo z= 3 +ai é uma raiz de p(x) , em que a é um número real positivo e i é a unidade imaginária, então o valor do produto k . a é igual a

A
44.
B
66.
C
24.
D
96.
33db9277-8a
UECE 2015 - Matemática - Números Complexos, Polinômios

O polinômio de menor grau, com coeficientes inteiros, divisível por 2x - 3, que admite x = 2i como uma das raízes e P(0) = -12 é

i é o número complexo cujo quadrado é igual a -1.

A
P(x) = 2x3 – 3x2 - 8x – 12.
B
P(x) = 2x3 + 3x2 - 8x – 12.
C
P(x) = - 2x3 – 3x2 - 8x – 12.
D
P(x) = 2x3 – 3x2 + 8x – 12.
690339f9-19
UNICAMP 2015 - Matemática - Polinômios

Considere o polinômio cúbico p(x) = x3 + x2 - ax - 3 , onde a é um número real. Sabendo que r e −r são raízes reais de p(x), podemos afirmar que p(1) é igual a

A
3.
B
1.
C
-2.
D
-4.
768377da-e2
FATEC 2011 - Matemática - Progressão Aritmética - PA, Funções, Logaritmos, Polinômios, Progressões

Considere a equação polinomial x3 − 9x2 + kx + 21 = 0, com k real. Se suas raízes estão em progressão aritmética, o valor de log2 (3k − 1)2 é

A
8.
B
10.
C
12.
D
16.
E
20.
b20ad803-a6
FGV 2015, FGV 2015 - Matemática - Polinômios

A equação algébrica ax3 + bx2 + cx + d = 0 possui coeficientes reais a, b, c, d, todos não nulos. Sendo x1 , x2 e x3 as raízes dessa equação, então  é igual a

A
-d/c
B
-c/d
C
-d/a
D
-a/b
E
-b/a
b215d992-a6
FGV 2015, FGV 2015 - Matemática - Polinômios

Observe o gráfico da função f no plano cartesiano.

                            

Dentre as expressões apresentadas nas alternativas a seguir, a única que pode corresponder à lei da função f é

A
f(x) = (x – 1)2 · (x – 2)2
B
f(x) = (x – 1)2 · (x – 2)2 · (x + 1) · (x + 2)
C
f(x) = (x2 – 1) · (x2 – 4)
D
f(x) = (x2 – 1) · (x2 – 4) · (x – 1)
E
f(x) = (x2 – 1) · (x2 – 4) · (x + 1)
b200729d-a6
FGV 2015, FGV 2015 - Matemática - Polinômios

Sabendo-se que o resto da divisão do polinômio P(x) = x3 – x2 + 2k + 2 por x – 3 é igual a 4k – 220, o valor de k é

A
–4.
B
–2.
C
2.
D
3.
E
4.
000e413a-39
PUC - PR 2014 - Matemática - Polinômios

Se (x - 2) é um fator do polinômio x³ + kx² + 12x - 8, então, o valor de k é igual a:

A
– 3.
B
2.
C
3.
D
6.
E
– 6.
77fc78b5-3d
FGV 2014 - Matemática - Polinômios

Considere o polinômio P(X) tal que  = x2+x+1. A soma de todas as raízes da equação P(3x) = 7 é igual a

A
-1/9
B
-1/3
C
0
D
5/9
E
5/3
d321176f-3b
PUC - RJ 2013 - Matemática - Polinômios

Sabendo que 1 é raiz do polinômio p(x) = 2x3 - ax2 - 2x, podemos afirmar que p(x) é igual a:

A
2x2(x -2)
B
2x(x - 1)(x + 1)
C
2x(x2 - 2)
D
x(x - 1)(x + 1)
E
x(2x2 - 2x - 1)
115613eb-36
UNESP 2010 - Matemática - Funções, Função de 1º Grau, Polinômios, Função de 2º Grau

Através dos gráficos das funções f(x) e g(x), os valores de f(g(0)) e g(f(1)) são, respectivamente:



A
–5 e 0.
B
–5 e 2.
C
0 e 0.
D
2 e –5.
E
2 e 0.