Questõessobre Polinômios
Considere a função polinomial ݂ f : ℝ → ℝ definida por
f ( x) = ax2 + bx + c,
em que a, b, c ∈ ℝ e a ≠ 0. No plano cartesiano xy ,a única intersecção da reta y = 2 com o gráfico de ݂f é o ponto (2;2) e a intersecção da reta x = 0 com o gráfico de ݂f é o ponto (0; - 6). O valor de a + b + c é
Considere a função polinomial ݂ f : ℝ → ℝ definida por
f ( x) = ax2 + bx + c,
em que a, b, c ∈ ℝ e a ≠ 0. No plano cartesiano xy ,a única intersecção da reta y = 2 com o gráfico de ݂f é o ponto (2;2) e a intersecção da reta x = 0 com o gráfico de ݂f é o ponto (0; - 6). O valor de a + b + c é
A soma e o produto das raízes do polinômio expresso por p(x) = (x3
+ 2x2
– 3x – 2)4
,
considerando-se suas multiplicidades, são, respectivamente,
Se P(x)=2x
4−x
2
– x+5 , então
P(-2) é:
A equação polinomial 2x³ - 3x² - 11x + 6 = 0 tem o conjunto solução S = {a, b, c} .
Pode-se afirmar que o valor de ( a + 1 )(b + 1)( c + 1) é:
Dado o polinômio p(x) = (x − 2)8 + (x − c)6
, em que c é uma constante, a soma de todas
as suas raízes, considerando-se suas multiplicidades, é igual a
A soma das raízes da equação x3 - 2x2 - 6x = 0 vale:
O polinômio P(x) = x3 - 3x2 + 7x - 5 possui uma raiz
complexa 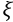 cuja parte imaginária é positiva. A parte real de
cuja parte imaginária é positiva. A parte real de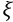 3 é igual a
3 é igual a
O polinômio P(x) = x3 - 3x2 + 7x - 5 possui uma raiz
complexa 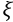 cuja parte imaginária é positiva. A parte real de
cuja parte imaginária é positiva. A parte real de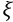 3 é igual a
3 é igual a
O gráfico a seguir, que passa pelos pontos
A,B,C e D, representa o polinômio P(x).

I O polinômio P(x) é um polinômio do segundo
grau.
II O polinômio D(x) = -3/4 x -3 é divisor de P(x)
III A reta que passa pelos pontos A e C intercepta o eixo das ordenadas no ponto (0, 11/2).
IV P(2) = P(-1/2)
Todas as afirmações corretas estão em:
O gráfico a seguir, que passa pelos pontos A,B,C e D, representa o polinômio P(x).

I O polinômio P(x) é um polinômio do segundo grau.
II O polinômio D(x) = -3/4 x -3 é divisor de P(x)
III A reta que passa pelos pontos A e C intercepta o eixo das ordenadas no ponto (0, 11/2).
IV P(2) = P(-1/2)
Todas as afirmações corretas estão em:
Se as raízes do polinômio P(x) = x3–12x2+ 47x –60 são reais, distintas e formam uma progressão aritmética, então, a soma dos cubos dessas raízes é igual a
Se os três números primos distintos p1, p2 e p3 são as raízes do polinômio p(x) = x3+ Hx2+ Kx + L, então, a soma dos inversos multiplicativos desses números é igual a
Um polinômio com coeficientes reais apresenta as seguintes
características:
- Uma raiz é 2+3i , em que i é a unidade imaginária.
- O número 1/2 é raiz de multiplicidade 2.
- −i é uma raiz, em que i é a unidade imaginária.
Podemos concluir que o menor grau que o polinômio pode ter é:
- Uma raiz é 2+3i , em que i é a unidade imaginária.
- O número 1/2 é raiz de multiplicidade 2.
- −i é uma raiz, em que i é a unidade imaginária.
Considerando os polinômios P(x) = 2x + b e Q(x) = ax² + 12x + 9 e sabendo que [P(x)]² = Q(x), determine o valor de a - b.
O polinômio P(x) é definido através do determinante
de uma matriz pela expressão:

O mesmo polinômio pode ser também representado por
O polinômio P(x) é definido através do determinante de uma matriz pela expressão:

O mesmo polinômio pode ser também representado por
Seja p(x) um polinômio de grau três tal que p(0)=6, p(1)=1, p(2)=4 e p(3)=9. É correto afirmar
que p(4) é igual a:
Considere o polinômio p(x) = x5 + bx3 + cx2 + d. Sabemos
que p(0) = 1, p(1) = 0 e p(-1) = 0.
Quanto vale p(2)?
Considere o polinômio p(x) = x5 + bx3 + cx2 + d. Sabemos que p(0) = 1, p(1) = 0 e p(-1) = 0.
Quanto vale p(2)?
Simplificando a expressão (a – 1)3 – (1 – a)2,
obtém-se um polinômio P(a). O coeficiente do termo de
maior grau de P(a) é:

Os dados na tabela se referem a um polinômio P(x), de grau 3, cuja soma das raízes
é igual a
