d878fcdd-73
USP 2021 - Matemática - Polinômios
Suponha que o polinômio p(x) = x3 + mx − 2, em que m é
um número real, tenha uma raiz real dupla a e uma raiz real
simples b. O valor da soma de m com a é:
Suponha que o polinômio p(x) = x3 + mx − 2, em que m é
um número real, tenha uma raiz real dupla a e uma raiz real
simples b. O valor da soma de m com a é:
A
0
B
–1
C
−2
D
−3
E
−4
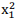 +
+ 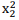 é igual a
é igual a , a
probabilidade de que a função f(x) seja estritamente crescente e seu gráfico intersecte o eixo y
em um valor maior ou igual a 2 é de
, a
probabilidade de que a função f(x) seja estritamente crescente e seu gráfico intersecte o eixo y
em um valor maior ou igual a 2 é de
