Questõessobre Polígonos
Acopla–se, exteriormente, a cada lado de um
triângulo retângulo um quadrado cujo lado é o
respectivo lado do triângulo, formando assim
uma figura plana composta do triângulo
retângulo e dos três quadrados, de tal modo que
cada quadrado tenha em comum com o triângulo
exatamente o lado ao qual está acoplado. A
medida dos catetos do triângulo são
respectivamente 6m e 8m. A figura será pintada.
Sabe-se que para pintar o quadrado menor usou-se 1,8 litros de tinta. Mantida a homogeneidade
da pintura, a quantidade de tinta necessária para
pintar toda a figura é
A Brazuca, a bola oficial da Copa é um cubo. Um cubo tem
______ faces, _______ arestas e _______ vértices (...). A Brazuca
é constituída por _______ peças, costuradas ao longo de
________ arestas e tem também _________ vértices. A única
diferença em relação a um cubo de verdade é que as arestas não
são retas, mas curvas. Um cubo esférico!
GHYS, Ethienne. In: Veja, 28 maio 2014. 21.
Quais são os inteiros que, respectivamente, preenchem
corretamente as lacunas do texto acima?
A Brazuca, a bola oficial da Copa é um cubo. Um cubo tem ______ faces, _______ arestas e _______ vértices (...). A Brazuca é constituída por _______ peças, costuradas ao longo de ________ arestas e tem também _________ vértices. A única diferença em relação a um cubo de verdade é que as arestas não são retas, mas curvas. Um cubo esférico!
GHYS, Ethienne. In: Veja, 28 maio 2014. 21.
Quais são os inteiros que, respectivamente, preenchem corretamente as lacunas do texto acima?
As bases de um trapézio têm como suporte as retas de equações
x − y −1 = 0 e
3y − 3x + 5 = 0.
A altura deste trapézio em cm é:
Sejam as afirmações:
( ) Os ângulos consecutivos de um paralelogramo são
suplementares.
( ) As bissetrizes dos ângulos opostos de um paralelogramo são
paralelas.
( ) O quadrado é, ao mesmo tempo, paralelogramo, retângulo e
losango.
Associando-se verdadeiro (V) ou falso (F) às afirmativas acima,
teremos:
A capacidade de um cilindro obtido através da rotação em torno do
lado menor de um retângulo de dimensões 3 cm e 4 cm é:
As abelhas, quando armazenam o mel, o
fazem em compartimentos individuais, de tal
maneira que formem um mosaico sem buracos
nem saliências entre as células, pois elas têm
que aproveitar o espaço ao máximo. Assim
estamos diante da seguinte questão: quais são
os polígonos regulares que se encaixam
perfeitamente sem deixar nenhum espaço vago
entre eles e que otimizam a quantidade de mel
armazenado nos seus correspondentes
mosaicos?
Uma condição necessária para que os
polígonos possam ser dispostos entre si sem
deixar espaços ou sobreposições é que a soma
da medida dos ângulos internos em torno de
cada vértice tem que ser 360º.
BASSANEZI, Rodney C. Ensino Aprendizagem com
Modelagem Matemática. Ed. Contexto. 2004, p. 214.
(Adaptado).
Assim, com relação ao formato das células
que constituem o mosaico, pode-se concluir
que:
Um retângulo tem vértices A, B, C e D. Se o lado AB é paralelo à reta x+2y-8=0 e C=(1,3), então, a reta
que contém o lado BC tem equação:
Sejam P e Q polígonos regulares. Se P é um
hexágono e se o número de diagonais do Q, partindo
de um vértice, é igual ao número total de diagonais
de P então a medida de cada um dos ângulos
internos de Q é
Uma reta paralela a um dos lados de um triângulo
equilátero intercepta os outros dois lados
determinando um triângulo menor e um trapézio, os
quais tem o mesmo perímetro. A razão entre a área
do triângulo menor e a área do trapézio é
Na figura, os segmentos OR e PQ são lados paralelos do quadrilátero
OPQR, e o vértice Q é o ponto em que a função f(x) = 2(−x2 + 4x) assume
seu maior valor.
 Sendo a área da região sombreada igual a 18u.a., pode-se afirmar que
uma equação cartesiana da reta r que contém o lado RQ do
quadrilátero é
Sendo a área da região sombreada igual a 18u.a., pode-se afirmar que
uma equação cartesiana da reta r que contém o lado RQ do
quadrilátero é

O número complexo 1 + i é raiz do polinômio P(x) = x4 + 3x3
+ px2 − 2x + q, com p,q ∈R.
Então, a soma das raízes reais de P(x) é
O número complexo 1 + i é raiz do polinômio P(x) = x4 + 3x3 + px2 − 2x + q, com p,q ∈R.
Então, a soma das raízes reais de P(x) é
Em 1772, o matemático Johann Titus e o astrônomo Johann Bode descobriram uma sequência
matemática nas distâncias dos planetas a partir do Sol — essa sequência previa a possibilidade
de um planeta orbitar entre Marte e Júpiter a 2,8 UA (unidades astronômicas) do Sol. Em 1801,
o astrônomo italiano Giuseppi Piazzi descobriu um corpo indistinto nessa distância, ao qual ele
deu o nome de Ceres, bem como outros corpos pequenos, nessa mesma adjacência, que foram
chamados de asteroides ou planetas anões.
Considerando-se que as distâncias dos planetas, a partir do Sol, são proporcionais aos termos
da sequência, de acordo com a tabela, pode-se afirmar que x é o quadrado de

Em um trapézio isósceles ABCD de bases AB e CD temos que AB=AD=10 cm. Sabendo-se que a base
CD mede 20 cm, determine o ângulo CAD.
O esquema apresenta as relações que certos quadriláteros notáveis possuem e que estão baseadas em algumas de suas
propriedades, representadas pelos números 1 e 2.
A propriedade 1 é compartilhada somente pelos retângulos e quadrados e não é compartilhada pelos losangos;
a propriedade 2 é compartilhada somente pelos losangos e quadrados e não é compartilhada pelos retângulos.
Com base nessas informações, é correto enunciar que a propriedade

O esquema apresenta as relações que certos quadriláteros notáveis possuem e que estão baseadas em algumas de suas propriedades, representadas pelos números 1 e 2.
A propriedade 1 é compartilhada somente pelos retângulos e quadrados e não é compartilhada pelos losangos; a propriedade 2 é compartilhada somente pelos losangos e quadrados e não é compartilhada pelos retângulos.
Com base nessas informações, é correto enunciar que a propriedade

Considere as seguintes afirmações:
I. Todo trapézio é um paralelogramo.
II. Todo paralelogramo é um trapézio.
III. Todo retângulo é um paralelogramo.
IV. Todo quadrado é losango, é retângulo, é paralelogramo e é trapézio
Considere as seguintes afirmações:
I. Todo trapézio é um paralelogramo.
II. Todo paralelogramo é um trapézio.
III. Todo retângulo é um paralelogramo.
IV. Todo quadrado é losango, é retângulo, é paralelogramo e é trapézio
No centro de uma pista de dança, foi construído um mosaico de led de 3 m × 3 m, dividido em nove
quadrados de lado 1 m. Em dois desses quadrados, foram inscritas duas circunferências, de acordo com
a figura a seguir.

Assinale a alternativa que apresenta, corretamente, a menor distância entre as duas circunferências
No centro de uma pista de dança, foi construído um mosaico de led de 3 m × 3 m, dividido em nove quadrados de lado 1 m. Em dois desses quadrados, foram inscritas duas circunferências, de acordo com a figura a seguir.

Assinale a alternativa que apresenta, corretamente, a menor distância entre as duas circunferências
A pintura, a seguir, de Kazimir Malevich tem como
título Retângulo preto, Triângulo azul e é um
exemplo do abstracionismo geométrico do início do
século XX, conhecido na Rússia como Suprematismo.

(kazimir-malevich.org/Suprematism-(with-Blue-Triangle-AndBlack-Rectangle).html. Acesso em: 01.10.2013. Original colorido)
Considere que as três informações a seguir são verdadeiras:
• O“Triângulo azul”é equilátero, com lados medindo 32 cm.
• O“Retângulo preto”tem dimensões de 30 cm x 60 cm.• Um dos lados do“Retângulo preto”intercepta os pontos
médios de dois lados do “Triângulo azul”.
É correto afirmar que a área da pintura ocupada pela composição
das figuras “Retângulo preto” e “Triângulo azul” é, em cm², igual a

A via de acesso a uma empresa será pavimentada por lajotas
hexagonais regulares. O projeto prevê que serão necessárias
fileiras com lajotas para cobrir seus 5,1 metros de largura,
conforme mostra o esquema a seguir.
Desconsiderando o espaço entre as lajotas, obtém-se que as
lajotas encomendadas deverão ter arestas cuja medida, em
centímetros, está entre

Seja ABCD um trapézio isósceles com ângulo 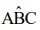 = 60º e com distância de 6 cm entre as
bases, como mostra a Figura 3.
= 60º e com distância de 6 cm entre as
bases, como mostra a Figura 3.

Figura 3: Trapézio isósceles
Sabendo que o prolongamento do lado CD do trapézio encontra-se com a mediatriz do lado BC
em um ponto E, de tal forma que o segmento 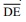 mede 10 cm, a área do trapézio é:
mede 10 cm, a área do trapézio é:
Seja ABCD um trapézio isósceles com ângulo 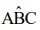 = 60º e com distância de 6 cm entre as
bases, como mostra a Figura 3.
= 60º e com distância de 6 cm entre as
bases, como mostra a Figura 3.

Figura 3: Trapézio isósceles
Sabendo que o prolongamento do lado CD do trapézio encontra-se com a mediatriz do lado BC
em um ponto E, de tal forma que o segmento 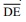 mede 10 cm, a área do trapézio é:
mede 10 cm, a área do trapézio é: