Questõessobre Polígonos
Na figura abaixo, destacamos as medidas de BC = 10 m e SR = 2,3 m. Os valores de x e y são:

Na figura abaixo, destacamos as medidas de BC = 10 m e SR = 2,3 m. Os valores de x e y são:

O valor do raio R do círculo inscrito no trapézio retângulo de bases 15 cm, 10 cm e lado oblíquo 13 cm, em cm,
é:
Na figura a seguir, o quadrilátero MNOP é um trapézio, os segmentos 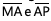 são congruentes e os segmentos
são congruentes e os segmentos 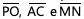 são paralelos. A
diferença entre as medidas dos segmentos
são paralelos. A
diferença entre as medidas dos segmentos 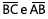 é igual a:
é igual a:

Na figura a seguir, o quadrilátero MNOP é um trapézio, os segmentos 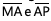 são congruentes e os segmentos
são congruentes e os segmentos 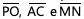 são paralelos. A
diferença entre as medidas dos segmentos
são paralelos. A
diferença entre as medidas dos segmentos 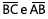 é igual a:
é igual a:

Considere o retângulo OPQR da figura a seguir:

A área S do retângulo em função da abscissa x do ponto R é:
Considere o retângulo OPQR da figura a seguir:

A área S do retângulo em função da abscissa x do ponto R é:
Na figura a seguir, 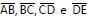 são congruentes e AEFJ é um trapézio
isósceles, com altura igual a 12 metros. Os segmentos
são congruentes e AEFJ é um trapézio
isósceles, com altura igual a 12 metros. Os segmentos 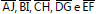 são paralelos e suas medidas formam uma progressão aritmética. Nessas
condições, pode-se afirmar que a soma das medidas dos segmentos
são paralelos e suas medidas formam uma progressão aritmética. Nessas
condições, pode-se afirmar que a soma das medidas dos segmentos 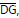
 é igual a:
é igual a:
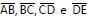 são congruentes e AEFJ é um trapézio
isósceles, com altura igual a 12 metros. Os segmentos
são congruentes e AEFJ é um trapézio
isósceles, com altura igual a 12 metros. Os segmentos 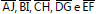 são paralelos e suas medidas formam uma progressão aritmética. Nessas
condições, pode-se afirmar que a soma das medidas dos segmentos
são paralelos e suas medidas formam uma progressão aritmética. Nessas
condições, pode-se afirmar que a soma das medidas dos segmentos 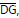
 é igual a:
é igual a:Os ângulos internos de um quadrilátero medem 3x - 45, 2x + 10, 2x + 15 e x + 20 graus. O menor ângulo mede:
.Um objeto de decoração tem a forma de um pentágono regular, apresentando todas as suas
diagonais. Sabe-se que cada diagonal foi pintada de uma cor diferente das demais. Então,
qual é o número de cores diferentes que foram utilizadas na pintura de tais diagonais?

Dois garotos estavam
conversando ao lado
de uma piscina, nas
posições A e B ,
como ilustra a figura ao
lado. O garoto que
estava na posição A
observou que o ângulo
BAˆ C era de 90º e que
as distâncias BD e
AD eram de 1m e 2m,
respectivamente.
Sabendo que o garoto da posição B gostava
de estudar geometria, o da posição A
desafiou-o a dizer qual era a largura da
piscina.
A resposta, correta, do garoto da posição B
deveria ser:

Dois garotos estavam conversando ao lado de uma piscina, nas posições A e B , como ilustra a figura ao lado. O garoto que estava na posição A observou que o ângulo BAˆ C era de 90º e que as distâncias BD e AD eram de 1m e 2m, respectivamente.
Sabendo que o garoto da posição B gostava de estudar geometria, o da posição A desafiou-o a dizer qual era a largura da piscina.
A resposta, correta, do garoto da posição B
deveria ser:
Um jornalista anuncia que, em determinado momento, o público presente em um comício
realizado numa praça com formato do trapézio isósceles , com bases medindo 100m e
140m (vide figura abaixo), era de 20.000 pessoas. Sabendo-se que  e, considerando-se
que em aglomerações desse tipo o número máximo de pessoas por metro quadrado é igual a 6,
o que pode ser concluído a respeito do anúncio jornalístico?
e, considerando-se
que em aglomerações desse tipo o número máximo de pessoas por metro quadrado é igual a 6,
o que pode ser concluído a respeito do anúncio jornalístico?

 e, considerando-se
que em aglomerações desse tipo o número máximo de pessoas por metro quadrado é igual a 6,
o que pode ser concluído a respeito do anúncio jornalístico?
e, considerando-se
que em aglomerações desse tipo o número máximo de pessoas por metro quadrado é igual a 6,
o que pode ser concluído a respeito do anúncio jornalístico? 
As intersecções das curvas de equações x2 + y2 - 7x - 9 = 0 e y2 = x + 2 são vértices de um polígono. A equação
da reta traçada pela intersecção das diagonais desse polígono, e paralela à reta de equação 2x - y + 3 = 0, é:
Na figura ao lado, ABCD é um quadrado de lado a. A
circunferência de raio x tangencia os lados AB e AD e a
semicircunferência de diâmetro CD.

O valor de x em função de a é
Na figura ao lado, ABCD é um quadrado de lado a. A circunferência de raio x tangencia os lados AB e AD e a semicircunferência de diâmetro CD.

O valor de x em função de a é





Um quadrilátero convexo ABCD tem ângulos retos nos vértices C e D, e as medidas dos lados  e
e  são iguais. Se E é um ponto qualquer do segmento
são iguais. Se E é um ponto qualquer do segmento  , distinto de A e de B, assinale a alternativa correta.
, distinto de A e de B, assinale a alternativa correta.
Se a medida de  é igual à medida de
é igual à medida de  , então a
medida da área do triângulo EBD é um quarto da
medida da área do quadrilátero ABCD.
, então a
medida da área do triângulo EBD é um quarto da
medida da área do quadrilátero ABCD.
Um quadrilátero convexo ABCD tem ângulos retos nos vértices C e D, e as medidas dos lados  e
e  são iguais. Se E é um ponto qualquer do segmento
são iguais. Se E é um ponto qualquer do segmento  , distinto de A e de B, assinale a alternativa correta.
, distinto de A e de B, assinale a alternativa correta.
 é igual à medida de
é igual à medida de  , então a
medida da área do triângulo EBD é um quarto da
medida da área do quadrilátero ABCD.
, então a
medida da área do triângulo EBD é um quarto da
medida da área do quadrilátero ABCD.Um quadrilátero convexo ABCD tem ângulos retos nos vértices C e D, e as medidas dos lados  e
e  são iguais. Se E é um ponto qualquer do segmento
são iguais. Se E é um ponto qualquer do segmento  , distinto de A e de B, assinale a alternativa correta.
, distinto de A e de B, assinale a alternativa correta.
A medida da área do triângulo CDE é igual à metade
da medida da área do quadrilátero ABCD para
qualquer posição do ponto E no segmento  .
.
Um quadrilátero convexo ABCD tem ângulos retos nos vértices C e D, e as medidas dos lados  e
e  são iguais. Se E é um ponto qualquer do segmento
são iguais. Se E é um ponto qualquer do segmento  , distinto de A e de B, assinale a alternativa correta.
, distinto de A e de B, assinale a alternativa correta.
 .
.Um quadrilátero convexo ABCD tem ângulos retos nos vértices C e D, e as medidas dos lados  e
e  são iguais. Se E é um ponto qualquer do segmento
são iguais. Se E é um ponto qualquer do segmento  , distinto de A e de B, assinale a alternativa correta.
, distinto de A e de B, assinale a alternativa correta.
A medida da área do triângulo CDE é igual à soma
das medidas das áreas dos triângulos ABC e BCD.
Um quadrilátero convexo ABCD tem ângulos retos nos vértices C e D, e as medidas dos lados  e
e  são iguais. Se E é um ponto qualquer do segmento
são iguais. Se E é um ponto qualquer do segmento  , distinto de A e de B, assinale a alternativa correta.
, distinto de A e de B, assinale a alternativa correta.
Um quadrilátero convexo ABCD tem ângulos retos nos vértices C e D, e as medidas dos lados  e
e  são iguais. Se E é um ponto qualquer do segmento
são iguais. Se E é um ponto qualquer do segmento  , distinto de A e de B, assinale a alternativa correta.
, distinto de A e de B, assinale a alternativa correta.
A medida de  é igual à medida de
é igual à medida de  .
.
Um quadrilátero convexo ABCD tem ângulos retos nos vértices C e D, e as medidas dos lados  e
e  são iguais. Se E é um ponto qualquer do segmento
são iguais. Se E é um ponto qualquer do segmento  , distinto de A e de B, assinale a alternativa correta.
, distinto de A e de B, assinale a alternativa correta.
 é igual à medida de
é igual à medida de  .
.Um quadrilátero convexo ABCD tem ângulos retos nos
vértices C e D, e as medidas dos lados  e
e  são
iguais. Se E é um ponto qualquer do segmento
são
iguais. Se E é um ponto qualquer do segmento  ,
distinto de A e de B, assinale a alternativa correta.
,
distinto de A e de B, assinale a alternativa correta.
Os ângulos  e
e  são ângulos retos.
são ângulos retos.
Um quadrilátero convexo ABCD tem ângulos retos nos
vértices C e D, e as medidas dos lados  e
e  são
iguais. Se E é um ponto qualquer do segmento
são
iguais. Se E é um ponto qualquer do segmento  ,
distinto de A e de B, assinale a alternativa correta.
,
distinto de A e de B, assinale a alternativa correta.
 e
e  são ângulos retos.
são ângulos retos.
Um retângulo R, de lados de medidas inteiras a cm e b cm, é dividido de modo a formar uma malha de quadrados de lado medindo 1 cm. Um raio de luz entra no retângulo R por um dos vértices, na direção da bissetriz do ângulo reto. Ao atingir o outro lado do retângulo R, esse raio é refletido e segue refletindo-se cada vez que toca em um lado do retângulo R. O raio de luz sai do retângulo R ao atingir um de seus vértices. O número inteiro positivo N de quadrados da malha que o raio de luz atravessa, desde a sua entrada até a sua saída, é o mínimo múltiplo comum entre a e b. Sobre o exposto, assinale o que for correto.
Se N = 30, então os lados do retângulo R medem 6
cm e 5 cm.
Se N = 30, então os lados do retângulo R medem 6 cm e 5 cm.