Questõessobre Poliedros
O sólido representado na figura é um tetraedro regular.

Assinale a alternativa que apresenta uma planificação de um tetraedro regular, em que cada lado comum a dois triângulos
representa uma aresta do tetraedro.
O sólido representado na figura é um tetraedro regular.

Assinale a alternativa que apresenta uma planificação de um tetraedro regular, em que cada lado comum a dois triângulos
representa uma aresta do tetraedro.





A respeito de um cubo inscrito numa superfície esférica de raio R:
I. O volume do cubo é maior que o volume da esfera.
II. O volume do cubo é: ν = 8 R3 /3√3 .
III. O comprimento da aresta do cubo é: a = √3 . R.
IV. O volume da esfera é igual ao volume do cubo.
A respeito de um cubo inscrito numa superfície esférica de raio R:
I. O volume do cubo é maior que o volume da esfera.
II. O volume do cubo é: ν = 8 R3 /3√3 .
III. O comprimento da aresta do cubo é: a = √3 . R.
IV. O volume da esfera é igual ao volume do cubo.
Considere as sentenças abaixo, e assinale (V) para verdadeira e (F) para falsa.
( ) Se o raio de uma esfera de raio 2 for multiplicado por 3, então o volume dessa esfera
também ficará multiplicado por 3.
( ) O produto das diagonais de um paralelepípedo reto retângulo de dimensões 4 cm, 2 cm
e 2 cm é igual a 576.
( ) Se um cilindro e um cone circular reto possuem a mesma altura e o raio do cilindro é o
dobro do raio do cone, então o volume do cilindro é 12 vezes maior que o volume do
cone.
Assinale a alternativa que contém a sequência correta, de cima para baixo.
Considere um cubo de aresta
a.
Os pontos I,
J, K, L, M e N são os centros das faces ABCD,
BCGF, DCGH, ADHE, ABFE e EFGH,
respectivamente, conforme representado na
figura abaixo.

O octaedro regular, cujos vértices são os
pontos I, J, K, L, M e N, tem aresta medindo
Considere um cubo de aresta a. Os pontos I, J, K, L, M e N são os centros das faces ABCD, BCGF, DCGH, ADHE, ABFE e EFGH, respectivamente, conforme representado na figura abaixo.

O octaedro regular, cujos vértices são os
pontos I, J, K, L, M e N, tem aresta medindo



Considere a planificação de um tetraedro,
conforme a figura abaixo.

Os triângulos ABC e ABD são isósceles
respectivamente em B e D. As medidas dos
segmentos  estão
indicadas na figura.
estão
indicadas na figura.
A soma das medidas de todas as arestas do
tetraedro é
Considere a planificação de um tetraedro, conforme a figura abaixo.

Os triângulos ABC e ABD são isósceles
respectivamente em B e D. As medidas dos
segmentos  estão
indicadas na figura.
estão
indicadas na figura.
A soma das medidas de todas as arestas do
tetraedro é
Considere ABCDEFGH paralelepípedo retoretângulo, indicado na figura abaixo, tal que  .
.

O volume do tetraedro AHFC é
Considere ABCDEFGH paralelepípedo retoretângulo, indicado na figura abaixo, tal que  .
.

O volume do tetraedro AHFC é
Considere um pentágono regular ABCDE de
lado 1. Tomando os pontos médios de seus
lados, constrói-se um pentágono FGHIJ, como
na figura abaixo.

A medida do lado do pentágono FGHIJ é
Considere um pentágono regular ABCDE de lado 1. Tomando os pontos médios de seus lados, constrói-se um pentágono FGHIJ, como na figura abaixo.

A medida do lado do pentágono FGHIJ é
Todas as faces de um cubo sólido de aresta 9 cm foram pintadas de verde. Em seguida, por meio de cortes paralelos
a cada uma das faces, esse cubo foi dividido em cubos menores, todos com aresta 3 cm. Com relação a esses
cubos, considere as seguintes afirmativas:
1. Seis desses cubos menores terão exatamente uma face pintada de verde.
2. Vinte e quatro desses cubos menores terão exatamente duas faces pintadas de verde.
3. Oito desses cubos menores terão exatamente três faces pintadas de verde.
4. Um desses cubos menores não terá nenhuma das faces pintada de verde.
Assinale a alternativa correta.
Todas as faces de um cubo sólido de aresta 9 cm foram pintadas de verde. Em seguida, por meio de cortes paralelos a cada uma das faces, esse cubo foi dividido em cubos menores, todos com aresta 3 cm. Com relação a esses cubos, considere as seguintes afirmativas:
1. Seis desses cubos menores terão exatamente uma face pintada de verde.
2. Vinte e quatro desses cubos menores terão exatamente duas faces pintadas de verde.
3. Oito desses cubos menores terão exatamente três faces pintadas de verde.
4. Um desses cubos menores não terá nenhuma das faces pintada de verde.
Assinale a alternativa correta.
Em 1958, como trote para os calouros da universidade de Harvard, nos Estados Unidos, um
grupo de estudantes precisou medir o comprimento da ponte de Harvard (entre Boston e
Cambridge, em Massachusetts), usando como padrão de medida um dos próprios estudantes,
um rapaz chamado Oliver R. Smoot. Após horas de medição, com o estudante deitando-se no
chão e levantando-se sucessivas vezes para as medidas, concluiu-se que a ponte tinha 364,4
smoots, +/- 1 orelha.
A brincadeira fez tanto sucesso e a medição tornou-se tão popular que, na década de 1980, a
ponte foi reformada pela prefeitura, que encomendou blocos de concreto personalizados de 1
smoot de comprimento para a reforma, eternizando as marcações colocadas no solo, que hoje
já constam até no sistema de conversão de medidas da ferramenta Google.
Ainda mais interessante é o fato de que, alguns anos após formado, Oliver Smoot tornou-se
diretor da ANSI, o Instituto Nacional Americano de Padrões (“American National Standards
Institute”) e depois presidente da ISO, a Organização Internacional para Padronização
(“International Organization for Standardization”).
Sabendo que Oliver Smoot tinha 5 pés e 7 polegadas de altura na ocasião da medida,
desprezando o erro de +/- 1 orelha, e assumindo 1 pé = 30,5 cm e 1 polegada = 2,5 cm, o
comprimento da ponte é:


Em um jogo matemático serão confeccionadas três peças, conforme figura a seguir:

A peça 1 é um prisma reto quadrangular cuja altura mede 4 cm e a base é um quadrado de 6 cm de lado. Do
centro dessa peça retirou-se um prisma reto de 4 cm de altura e cuja base é um triângulo equilátero de
lado 2 cm.
A peça 2 é um cilindro reto de 6 cm de diâmetro e 4 cm de altura. Do centro dessa peça retirou-se um
prisma reto de 4 cm de altura e cuja base é um quadrado de lado 2 cm.
A peça 3 é um prisma reto triangular cuja altura mede 4 cm e a base é um triângulo equilátero de 6 cm de
lado. Do centro dessa peça retirou-se um cilindro reto de 4 cm de altura e cujo diâmetro mede 2 cm.
Utilizando o mesmo material para confeccionar essas peças e adotando π=3,1 e √3 = 1,7 , é correto afirmar
que
Em um jogo matemático serão confeccionadas três peças, conforme figura a seguir:

A peça 1 é um prisma reto quadrangular cuja altura mede 4 cm e a base é um quadrado de 6 cm de lado. Do centro dessa peça retirou-se um prisma reto de 4 cm de altura e cuja base é um triângulo equilátero de lado 2 cm.
A peça 2 é um cilindro reto de 6 cm de diâmetro e 4 cm de altura. Do centro dessa peça retirou-se um prisma reto de 4 cm de altura e cuja base é um quadrado de lado 2 cm.
A peça 3 é um prisma reto triangular cuja altura mede 4 cm e a base é um triângulo equilátero de 6 cm de lado. Do centro dessa peça retirou-se um cilindro reto de 4 cm de altura e cujo diâmetro mede 2 cm.
Utilizando o mesmo material para confeccionar essas peças e adotando π=3,1 e √3 = 1,7 , é correto afirmar que
Uma agência de viagens decidiu presentear cada pessoa que comprou uma passagem, no mês de março, para
assistir aos jogos da Copa do Mundo de 2010. O brinde oferecido consistia de uma minibola de futebol, pintada com as
cores da bandeira da África do Sul e embalada em uma caixa de presente. Assuma que a caixa (com tampa) tenha o
formato de um cubo, a minibola tenha o formato de uma esfera e que esteja perfeitamente inscrita na caixa.
Sabe-se que:
1 - A agência vendeu 50 passagens em março, destinadas a pessoas que fossem assistir aos jogos;
2 - A fábrica que produziu a minibola e a caixa estimou seus custos na produção de cada unidade. Desta forma,
cobrou de cada caixa o valor equivalente a R$ 0,01 por cm2
de sua área e, de cada minibola, o valor equivalente a
R$ 0,02 por cm2 de sua área.
Se a diagonal da caixa mede √300cm, utilizando a aproximação π = 3,1, pode-se afirmar que o gasto aproximado
da agência com todos os brindes ofertados em março foi de:
O número de cubos, cuja medida das arestas
é 10 cm, necessário para formar um paralelepípedo
cujas medidas das arestas são 0,9 m; 1,1 m e 1,0 m
é
Considerando essas informações e que o número de Avogadro seja igual a 6,0 × 1023, julgue o item que é do tipo C.
A razão entre o volume do cubo e o volume do octaedro é
igual a
6.
Considerando essas informações e que o número de Avogadro seja igual a 6,0 × 1023, julgue o item que é do tipo C.
A razão entre o volume do cubo e o volume do octaedro é igual a
6.

Em 2013, uma das descobertas de maior importância do
ponto de vista tecnológico foi a criação de unidades fotovoltaicas
à base de perovskita, termo que designa um tipo de óxido com
fórmula geral ABO3, em que A e B representam cátions metálicos.
Um exemplo típico é o CaTiO3. A unidade básica do cristal de uma
perovskita consiste na estrutura cúbica mostrada na figura acima,
em que cada um de oito cátions “A” ocupa um dos vértices do cubo;
seis íons oxigênio estão nos centros das faces do cubo, formando
um octaedro regular; e um cátion “B” está no centro do cubo.
As luminárias para um laboratório de matemática
serão fabricadas em forma de sólidos geométricos.
Uma delas terá a forma de um tetraedro truncado.
Esse sólido é gerado a partir de secções paralelas
a cada uma das faces de um tetraedro regular.
Para essa luminária, as secções serão feitas de
maneira que, em cada corte, um terço das arestas
seccionadas serão removidas. Uma dessas secções
está indicada na figura.

Essa luminária terá por faces

Considere o sólido obtido pela revolução do
retângulo ABCD em torno da reta r ,
conforme indicado na figura a seguir.

O volume do sólido obtido é
Considere o sólido obtido pela revolução do retângulo ABCD em torno da reta r , conforme indicado na figura a seguir.

O volume do sólido obtido é
NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:
N: Conjunto dos números naturais.
R: Conjunto dos números reais.
Na figura a seguir, está representado um
cubo cuja aresta tem 2 cm de medida. O
ponto P está localizado no centro da face
EFGH .

A medida do segmento 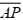 é
é
Na figura a seguir, está representado um cubo cuja aresta tem 2 cm de medida. O ponto P está localizado no centro da face EFGH .

A medida do segmento 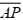 é
é
NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:
N: Conjunto dos números naturais.
R: Conjunto dos números reais.
Assinale a opção que corresponde à medida da
altura do tetraedro regular cuja medida da aresta é
igual a 3 m.



Uma lesma mora na superfície de um sólido com o formato de um
tetraedro regular ABCD, cujas arestas têm, cada uma, comprimento L.
A lesma se encontra no ponto médio da aresta AB e deseja viajar até o
ponto médio da aresta CD. A menor distância que ela pode percorrer
nessa viagem é

