8123d4ad-df
UFMT 2008 - Matemática - Números Complexos
A imagem do número complexo z = 5 + i√3 é um vértice de um
hexágono regular com centro na origem. O outro vértice desse
hexágono, que também está localizado no primeiro quadrante, é a
imagem do número complexo:
A imagem do número complexo z = 5 + i√3 é um vértice de um
hexágono regular com centro na origem. O outro vértice desse
hexágono, que também está localizado no primeiro quadrante, é a
imagem do número complexo:
A
2 + 3i√3
B
1+ 2i√3
C
2 + 2i√3
D
3 + 3i√3
E
1+ 3i√3
 e
e  , é correto afirmar
que o menor valor inteiro positivo de n que torna
, é correto afirmar
que o menor valor inteiro positivo de n que torna  um número real positivo é
um número real positivo é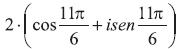 escrito na forma algébrica é
escrito na forma algébrica é


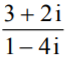 na forma x + y i é
na forma x + y i é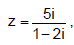 considere o número complexo w com módulo igual ao de z e argumento
principal medindo o dobro do argumento principal de z.
Nessas condições, w pode ser representado algebricamente por
considere o número complexo w com módulo igual ao de z e argumento
principal medindo o dobro do argumento principal de z.
Nessas condições, w pode ser representado algebricamente por




 um número real positivo é
um número real positivo é