Questõessobre Números Complexos
Se Z é um número
complexo satisfazendo |z + 6| ≤ 4 podemos garantir que o maior valor de
|z + 2| 2 é:
Sejam x,y,z e w números inteiros tais que x < 2y, y < 3z e z < 4w.
Se w < 10, então o maior valor possível para x é
Sejam x,y,z e w números inteiros tais que x < 2y, y < 3z e z < 4w.
Se w < 10, então o maior valor possível para x é
No plano de Argand-Gauss a seguir está representado o polígono
ABCDEF que deverá sofrer uma rotação de 90o
no sentido anti-horário
em torno do ponto A, formando o polígono AB’C’D’E’F’.

Nessas condições, pode-se afirmar que a soma A + B’ + C’ + D’ + E’ + F’
é igual ao número complexo:
No plano de Argand-Gauss a seguir está representado o polígono ABCDEF que deverá sofrer uma rotação de 90o no sentido anti-horário em torno do ponto A, formando o polígono AB’C’D’E’F’.

Nessas condições, pode-se afirmar que a soma A + B’ + C’ + D’ + E’ + F’
é igual ao número complexo:
Sejam os números reais x = 5/12 , y = 12/29 e z = 7/17 .
Assinale a opção correta:
Sejam os números reais x = 5/12 , y = 12/29 e z = 7/17 .
Assinale a opção correta:
Quatro números complexos representam, no plano complexo, vértices de um paralelogramo. Três dos números
são z= -3 - 3i, z2 = 1 e z3 = -1 + (5/2)i. O quarto número tem as partes real e imaginária positivas. Esse número é
Dado o número complexo 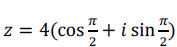 , na sua forma trigonométrica, calculando
a potência z3, a forma algébrica dessa potência é:
, na sua forma trigonométrica, calculando
a potência z3, a forma algébrica dessa potência é:
Dado o número complexo 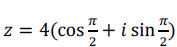 , na sua forma trigonométrica, calculando
a potência z3, a forma algébrica dessa potência é:
, na sua forma trigonométrica, calculando
a potência z3, a forma algébrica dessa potência é:
Quatro números complexos representam, no plano complexo, vértices de um paralelogramo. Três dos números
são z= -3 - 3i, z2‚ = 1 e z3 = -1 + (5/2)i. O quarto número tem as partes real e imaginária positivas. Esse número é
Seja n um número natural, e os conjuntos:
A = { x ∈  / x = 2n }
/ x = 2n }
B = { x ∈ / x = 3n }
/ x = 3n }
C = { x ∈  / x = 5n }
/ x = 5n }
Leia atentamente os itens abaixo:
I) n.(n + 1), para todo n natural, é um
elemento de A.
II) n³ – n, para todo n natural, não é um
elemento de B.
III) 5n5 – 5n², para todo n natural, é um
elemento de (A ∪ B ∪ C).
Assinale a alternativa correta:
Seja n um número natural, e os conjuntos:
A = { x ∈  / x = 2n }
/ x = 2n }
B = { x ∈ / x = 3n }
/ x = 3n }
C = { x ∈  / x = 5n }
/ x = 5n }
Leia atentamente os itens abaixo:
I) n.(n + 1), para todo n natural, é um elemento de A.
II) n³ – n, para todo n natural, não é um elemento de B.
III) 5n5 – 5n², para todo n natural, é um elemento de (A ∪ B ∪ C).
Assinale a alternativa correta:
Leia o texto e siga as orientações:
• pense em um número inteiro positivo N, de três algarismos distintos e não nulos;
• com os algarismos de N, forme todos os possíveis números de dois algarismos distintos;
• obtenha a soma (S) de todos esses números de dois algarismos;
• obtenha a soma (R) dos três algarismos do número N;
• finalmente, divida S por R.
O quociente da divisão de S por R é igual a
Considere os números complexos 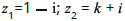 , com k um
número real positivo e
, com k um
número real positivo e 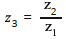 . Sabendo que
. Sabendo que 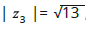 , é
correto afirmar:
, é
correto afirmar:
Considere os números complexos 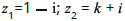 , com k um
número real positivo e
, com k um
número real positivo e 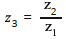 . Sabendo que
. Sabendo que 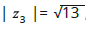 , é
correto afirmar:
, é
correto afirmar:





Considere as afirmações abaixo.
I - x2 ≥ x, para todo número real x.
II- -2x-6/x-12 ≥ 0, para todo x número real no
intervalo [2, 11].
III- √x2 + 2x + 1 = x + 1, para todo número
real x.
Assinale a alternativa correta.
Considere as afirmações abaixo.
I - x2 ≥ x, para todo número real x.
II- -2x-6/x-12 ≥ 0, para todo x número real no intervalo [2, 11].
III- √x2 + 2x + 1 = x + 1, para todo número real x.
Assinale a alternativa correta.
Admitindo que o centro do plano complexo coincida com o centro de um relógio analógico, se o ponteiro dos
minutos tiver 4 unidades de comprimento, estará, às 16 horas e 50 minutos, sobre o número complexo
O módulo do número complexo z =
2√3 + 2i
é igual a:
Se x e y são números reais não nulos, pode-se
afirmar corretamente que o módulo do número
complexo z =
x - iy /x + iy é igual a
Um número complexo z = a + lb está (a,b) representado geometricamente por um ponto
cuja distância da origem O é de uma unidade, e
o segmento OP faz um ângulo de 15º com o eixo dos x
(abcissas). Então, o número complexo z4 é
representado por um ponto Q = (x,y), tal que
Uma trinômio do segundo grau p(x) = x² + bx + c tem como raiz o número complexo 2 - 5i .
Então, o valor de (b + c) é
Seja M o conjunto formado pelos sete meios geométricos positivos
entre √2 e 16 √2 . A soma dos elementos de M que pertencem ao
conjunto dos números racionais é:
Se x é um número real, de modo que | x+1 | < 2 e | x-2 | < 2 , então x pertence ao intervalo real
Considere os seguintes números complexos  , em que j é a unidade
imaginária igual a √-1. São feitas as seguintes afirmações:
, em que j é a unidade
imaginária igual a √-1. São feitas as seguintes afirmações:
I – O módulo de Z1 . Z2 é igual a 4.
II – A forma trigonométrica de  é dada por:
é dada por: 
III – Z12 é um número imaginário puro e Z23 é um número real.
Assinale a alternativa correta:
Considere os seguintes números complexos  , em que j é a unidade
imaginária igual a √-1. São feitas as seguintes afirmações:
, em que j é a unidade
imaginária igual a √-1. São feitas as seguintes afirmações:
I – O módulo de Z1 . Z2 é igual a 4.
II – A forma trigonométrica de  é dada por:
é dada por: 
III – Z12 é um número imaginário puro e Z23 é um número real.
Assinale a alternativa correta: