fe0d9eed-a5
UNB 2011 - Matemática - Números Complexos
Com base nessas informações e considerando o centímetro como a unidade de medida de comprimento, em ambos os eixos, julgue os itens de 18 a 21 e assinale a opção correta no item 22, que é do tipo C.
Se z1 corresponde ao ponto C e se z2 corresponde ao ponto B, então 
Com base nessas informações e considerando o centímetro como a unidade de medida de comprimento, em ambos os eixos, julgue os itens de 18 a 21 e assinale a opção correta no item 22, que é do tipo C.
Se z1 corresponde ao ponto C e se z2 corresponde ao ponto B, então
Se z1 corresponde ao ponto C e se z2 corresponde ao ponto B, então


C
Certo
E
Errado
 O quarto número tem as partes real e imaginária positivas. Esse número é
O quarto número tem as partes real e imaginária positivas. Esse número é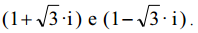
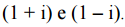
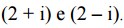
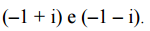
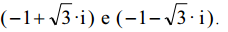
 R, e i 2 = –1. Para indicar a posição (x1,y1) e a distância d, da origem ao cofre, a pessoa escreveu no final do mapa: x1 + y1 = (1 + y) 9.
R, e i 2 = –1. Para indicar a posição (x1,y1) e a distância d, da origem ao cofre, a pessoa escreveu no final do mapa: x1 + y1 = (1 + y) 9. 



