Questõesde FGV sobre Matrizes

InícioTodas as questões
1
1
1
Foram encontradas 13 questões
4e1ca13b-fd
FGV 2015 - Matemática - Matrizes, Álgebra Linear

Seja a matriz A= cujo determinante é igual a 8. Nessas condições, o determinante da matriz 2A será igual a

A
128
B
32
C
64
D
16
E
256
3e5ee22e-fc
FGV 2020 - Matemática - Matrizes, Álgebra Linear

A matriz X tal que A.X  =B , em que 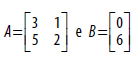  , tem como soma de seus elementos o valor:

A
12
B
27
C
16
D
18
E
14
139b3771-de
FGV 2014, FGV 2014 - Matemática - Matrizes, Álgebra Linear

4 Sejam as matrizes e B =[5 8]. A matriz X que satisfaz a equação matricial XA = B tem elementos cuja soma é

A
0,5
B
1
C
1,5
D
2
E
2,5
2dc5bc51-d8
FGV 2014 - Matemática - Matrizes, Álgebra Linear

O sistema de equações nas incógnitas x, y e z dado pela equação matricial

A
possível e determinado para qualquer valor de m.
B
possível e determinado somente para m = 4.
C
impossível para m = –2.
D
indeterminado para m = 2 ou m = –2.
E
indeterminado apenas para m = 2.
1d542a97-b0
FGV 2015 - Matemática - Matrizes, Álgebra Linear

Os pontos de coordenadas (x-y) do plano cartesiano que satisfazem a equação matricial  representam:

A
uma elipse com centro no ponto (0,0).
B
um par de retas paralelas com declividade – 3.
C
uma hipérbole com um dos focos de coordenadas (–3,0).
D
uma circunferência de raio √2/2.
E
uma parábola com concavidade voltada para cima.
29cacacd-1c
FGV 2016 - Matemática - Matrizes, Álgebra Linear

Uma matriz A de ordem 2 transmite uma palavra de 4 letras em que cada elemento da matriz representa uma letra do alfabeto. A fim de dificultar a leitura da palavra, por se tratar de informação secreta, a matriz A é multiplicada pela matriz obtendo-se a matriz codificada B.A.

Sabendo que a matriz B.A é igual a , podemos afirmar que a soma dos elementos da matriz A é:

A
46
B
48
C
49
D
47
E
50
618c7552-16
FGV 2018 - Matemática - Matrizes, Álgebra Linear

Se A, B e C forem matrizes quadradas de ordem 2, que possuem inversa, e se 0 for a matriz nula quadrada de ordem 2, podemos afirmar que:

A
Os produtos AB e BA sempre existem mas nunca AB = BA.
B
Se BC = 0, então B = 0 ou C = 0.
C
A2 - C2 = (A + C)(A - C)
D
Se CA = CB, então A = B.
E
(A + B)2 = A2 +2AB + B2
b0515e4a-15
FGV 2018 - Matemática - Matrizes, Álgebra Linear

Se A, B e C forem matrizes quadradas de ordem 2, que possuem inversa, e se O for a matriz nula quadrada de ordem 2, podemos afirmar que:

A
Os produtos AB e BA sempre existem mas nunca AB = BA.
B
Se BC = 0, então B = 0 ou C = 0.
C
A2 - C2 = (A + C)(A − C)
D
Se CA = CB, então A = B.
E
(A + B)2 = A2 + 2AB + B2
3661b81c-42
FGV 2016 - Matemática - Matrizes, Álgebra Linear

Dada a matriz e sabendo que a matriz é a matriz inversa da matriz A, podemos concluir que a matriz X, que satisfaz a equação matricial AX = B , tem como soma de seus elementos o número

A
14
B
13
C
15
D
12
E
16
35806ada-c0
FGV 2016 - Matemática - Matrizes, Álgebra Linear

Dada a matriz e sabendo que a matriz é a matriz inversa da matriz A, podemos concluir que a matriz X, que satisfaz a equação matricial AX = B , tem como soma de seus elementos o número

A
14
B
13
C
15
D
12
E
16
b220b08d-a6
FGV 2015, FGV 2015 - Matemática - Matrizes

Os marcos A, B, C e D de uma cidade estão conectados por pistas de rodagem, conforme mostra a malha viária indicada no diagrama da figura 1. A figura 2 indica uma matriz que representa as quantidades de caminhos possíveis de deslocamento entre os marcos (dois a dois). Considera-se um caminho entre dois marcos qualquer percurso que não viole o sentido da pista, que não passe novamente pelo marco de onde partiu e que termine quando se atinge o marco de destino final pela primeira vez. As flechas da figura 1 indicam o sentido das pistas de rodagem.

                        

Durante período de obras na malha viária descrita, a pista de rodagem entre os marcos A e D passou a ser de mão simples (sentido de A para D), e a pista do marco C para o marco D, ainda que tenha permanecido com mão simples, teve seu sentido invertido, passando a ser de D para C. Comparando os 16 elementos da matriz da figura 2 com seus correspondentes na matriz da nova configuração de malha viária, a quantidade de elementos que mudarão de valor é igual a

A
5.
B
6.
C
7.
D
8.
E
9.
77ed1f11-3d
FGV 2014 - Matemática - Matrizes, Álgebra Linear

Os elementos da matriz A = (aij)3x3 representam a quantidade de voos diários apenas entre os aeroportos i, de um país, e os aeroportos j, de outro país. A respeito desses voos, sabe-se que:

✓ quando j=2, o número de voos é sempre o mesmo,

✓ quando i=j, o número de voos é sempre o mesmo,

✓ quando i=3, o número de voos é sempre o mesmo;

✓ a11 ≠ 0, e det A = 0.

De acordo com as informações, é correto afirmar que o conjunto solução com as possibilidades de a11 é igual a

A
{a21 , a13}
B
{a21 , a23}
C
{a22 , a13}
D
{a21 , a22}
E
{a13 , a22}
982587de-fe
FGV 2014 - Matemática - Matrizes, Álgebra Linear

Quatro ônibus (representados por 1, 2, 3 e 4) levaram torcedores de um time de futebol para assistir a um jogo em outra cidade. Cada um deles tinha capacidade para 46 passageiros. Durante uma parada, todos os torcedores saíram dos ônibus, mas quando retornaram, vários torcedores não entraram no mesmo ônibus de onde tinham saído. Além disso, o ônibus 4 apresentou defeito, não pôde continuar a viagem e seus ocupantes tiveram que se acomodar nos três ônibus restantes.

Na matriz A, abaixo, cada elemento aij representa o número de pessoas que saíram do ônibus i e, após a parada, entraram no ônibus j.



Então, é correto concluir que,

A
depois da parada, o ônibus 1 ficou com 14 passageiros a mais.
B
depois da parada, o ônibus 2 ficou com 13 passageiros a mais.
C
depois da parada, o ônibus 3 ficou com 11 passageiros a mais.
D
antes da parada, dois ônibus tinham a mesma quantidade de passageiros.
E
depois da parada, um ônibus ficou lotado.