Seja a matriz M =  Se M–1 é a matriz inversa de M,
det(M–1) é:
Se M–1 é a matriz inversa de M,
det(M–1) é:
Seja a matriz M =  Se M–1 é a matriz inversa de M,
det(M–1) é:
Se M–1 é a matriz inversa de M,
det(M–1) é:
Seja a matriz M =  Se M–1 é a matriz inversa de M,
det(M–1) é:
Se M–1 é a matriz inversa de M,
det(M–1) é:
Seja a matriz M =  Se M–1 é a matriz inversa de M,
det(M–1) é:
Se M–1 é a matriz inversa de M,
det(M–1) é:
 e a função f : R → R definida por
f(x) = 1/3 det(A). Se f(3) = 3, o valor de k é:
e a função f : R → R definida por
f(x) = 1/3 det(A). Se f(3) = 3, o valor de k é:Sejam  matrizes e f uma função dada por
f(x) = x2
– 2x + 3; então f(A) é:
matrizes e f uma função dada por
f(x) = x2
– 2x + 3; então f(A) é:





Sejam  matrizes e f uma função dada por
f(x) = x2
– 2x + 3; então f(A) é:
matrizes e f uma função dada por
f(x) = x2
– 2x + 3; então f(A) é:





 .Se M–1 é a matriz inversa de M,
det(M–1) é:
.Se M–1 é a matriz inversa de M,
det(M–1) é: e a função f : R → R definida por
f(x) = 3
1
det(A). Se f(3) = 3, o valor de k é:
e a função f : R → R definida por
f(x) = 3
1
det(A). Se f(3) = 3, o valor de k é:Dadas as matrizes 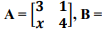
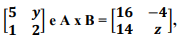 então 3x – y + 2z vale:
então 3x – y + 2z vale:
Sejam as matrizes A = 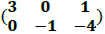 e B =
e B = 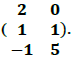 O determinante da matriz A x B vale:
O determinante da matriz A x B vale:

Sabendo-se que a matriz:

é igual à sua transposta, o valor de 2x + y é

Considere a seguinte matriz:  . Os valores de x para que det(2A) = 32 são:
. Os valores de x para que det(2A) = 32 são:



Para codificar palavras de 4 letras, por meio de matrizes, pode-se utilizar o seguinte método:
I) Associa-se cada letra da palavra a um número da tabela:

II) Escreve-se, com os números obtidos, uma matriz M de ordem 2 × 2.
Exemplo: A matriz correspondente à palavra BOTA é M = 
III) Multiplica-se M pela matriz-codificadora (C), inversível de ordem 2, obtendo-se, assim, a matriz-codificada N = C.M;
IV) Para obter a matriz M, calcula-se o produto C-1.N.
Uma palavra com quatro letras fora codificada pelo método acima obtendo-se a matriz N = 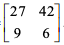 . Sabendo-se que a
matriz-codificadora utilizada foi C =
. Sabendo-se que a
matriz-codificadora utilizada foi C =  , pode-se afirmar que essa palavra é:
, pode-se afirmar que essa palavra é:
AMOR
VIDA
UNIR
ROSA
FLOR
Seja A = aij a matriz quadrada de ordem 3 definida
por aij = 
Dois alunos estavam trabalhando com a sequência 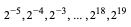 , quando um
outro aluno aproveitou a oportunidade e construiu uma matriz
, quando um
outro aluno aproveitou a oportunidade e construiu uma matriz 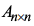 com esses números, sem
repetir qualquer deles. Depois disso, lançou um desafio aos amigos, perguntando a relação entre
e
com esses números, sem
repetir qualquer deles. Depois disso, lançou um desafio aos amigos, perguntando a relação entre
e 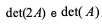 . Qual a resposta a esse desafio?
. Qual a resposta a esse desafio?





É possível B ser igual a kA.