Dadas as matrizes 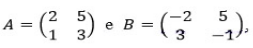 o produto entre a matriz inversa de A e a matriz transposta de B é a matriz
o produto entre a matriz inversa de A e a matriz transposta de B é a matriz
Dadas as matrizes 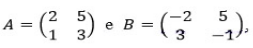 o produto entre a matriz inversa de A e a matriz transposta de B é a matriz
o produto entre a matriz inversa de A e a matriz transposta de B é a matriz





Dadas as matrizes 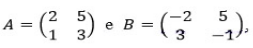 o produto entre a matriz inversa de A e a matriz transposta de B é a matriz
o produto entre a matriz inversa de A e a matriz transposta de B é a matriz





Assinale a alternativa que representa o valor de x na igualdade 
Considere a matriz

A soma das raízes da equação det(M2) = 25 é igual a:
Dada a matriz A = 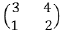 , o determinante de A5 é igual a:
, o determinante de A5 é igual a:
Considere a matriz A =  sendo a, b,c e d números reais. As retas r: y = ax + b e s: y = cx + d são perpendiculares entre si, a
reta r contém o ponto (2, 3) e a reta s contém o
ponto (0,0). Assim, o determinante da
matriz A é
sendo a, b,c e d números reais. As retas r: y = ax + b e s: y = cx + d são perpendiculares entre si, a
reta r contém o ponto (2, 3) e a reta s contém o
ponto (0,0). Assim, o determinante da
matriz A é
Se x é um número real positivo tal que

e det (A.B) = 2, então x-x é igual a
 respeitam a seguinte lei de formação para os seus
respeitam a seguinte lei de formação para os seus 


Considere as matrizes A = (aij)
2×3
, com aij = 2i – j, B=  e C=
e C=  , sendo m um número real. Sabendo que
C = A · B, então det C é igual a
, sendo m um número real. Sabendo que
C = A · B, então det C é igual a
Dada a matriz A=  ,
quadrada de ordem 3, pode-se afirmar
,
quadrada de ordem 3, pode-se afirmar
A matriz B é dada por 
AxB = 
 é simétrica.
é simétrica.  é simétrica
é simétrica é
é As operações de soma, multiplicação e cálculo do determinante de matrizes podem ser realizadas dependendo da ordem das matrizes envolvidas. Com base na ordem das matrizes A2X3, B3X2 e C2X2, considere verdadeiras (V) ou falsas (F) as afirmações que seguem.
( ) É possível multiplicar as matrizes A e B, nessa ordem, e também somá-las.
( ) É possível multiplicar as matrizes A e C.
( ) É possível calcular o determinante da matriz C.
Marque a alternativa que preenche corretamente os parênteses, de cima para baixo.

 corresponde à média
corresponde à média Uma empresa vende três produtos P1 , P2 e P3 cujos preços de venda, em unidades monetárias, estão respectivamente representados pelos termos a1j, j ∈{1, 2, 3}, da matriz A= (63 90 70); o número de unidades de cada produto, vendidas em um determinado mês está representado pelos termos b1j, j ∈{1, 2, 3}, da matriz B = (45 25 35), e o custo de produção de cada produto, está representado pelos termos c1j, j ∈{1, 2, 3}, da matriz C = (55 70 58). Com base nessas informações, é correto afirmar:
O lucro total pode ser obtido por meio da expressão matricial (A – C)Bt
.
Em C, o conjunto solução da equação  é
é
Considere a seguinte matriz quadrada:

É correto afirmar que:
 , em que A2 = A . A .
, em que A2 = A . A .