Seja a matriz A=  cujo determinante é igual a 8.
Nessas condições, o determinante da matriz 2A será igual a
cujo determinante é igual a 8.
Nessas condições, o determinante da matriz 2A será igual a
Seja a matriz A=  cujo determinante é igual a 8.
Nessas condições, o determinante da matriz 2A será igual a
cujo determinante é igual a 8.
Nessas condições, o determinante da matriz 2A será igual a
Seja a matriz A=  cujo determinante é igual a 8.
Nessas condições, o determinante da matriz 2A será igual a
cujo determinante é igual a 8.
Nessas condições, o determinante da matriz 2A será igual a
Se M é uma matriz tal que M² =  , então det (M−1) é igual a
, então det (M−1) é igual a
Dadas as matrizes A =  , sabe-se que A . B = C. Está correto afirmar que xy
é igual a:
, sabe-se que A . B = C. Está correto afirmar que xy
é igual a:
Determine a solução da inequação  dentre as apontadas nas alternativas a seguir.
dentre as apontadas nas alternativas a seguir.
Dada a matriz 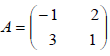 e sabendo que a matriz B é igual à transposta de A, ou seja, B = A t o determinante da matriz X dada por X = AB, é
e sabendo que a matriz B é igual à transposta de A, ou seja, B = A t o determinante da matriz X dada por X = AB, é
O par ordenado (x, y) que é solução da equação matricial  satisfaz também a
equação
satisfaz também a
equação
Considere as matrizes M =  e N =
e N = 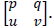 Se M.N = N.M, é correto afirmar que o determinante da matriz N é igual a
Se M.N = N.M, é correto afirmar que o determinante da matriz N é igual a

Observe a matriz A, quadrada e de ordem três.

Considere que cada elemento aij dessa matriz é o valor do logaritmo decimal de (i + j). O valor de x é igual a:
Dadas as matrizes X e Y, sabendo-se que X=Yt,onde Yt é a matriz transposta de Y.

Podemos afirmar que o valor de a e b são iguais a
A matriz X tal que A.X =B , em que 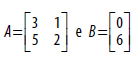 , tem
como soma de seus elementos o valor:
, tem
como soma de seus elementos o valor:
Dadas as matrizes o valor de
o valor de  é igual a :
é igual a :
As coordenadas de um ponto P, no plano cartesiano, são
(a,b) = (1,1).  é uma matriz de rotação, P’ = M × P. Assinale a alternativa que apresenta as
coordenadas de P’, para α = π/
6.
é uma matriz de rotação, P’ = M × P. Assinale a alternativa que apresenta as
coordenadas de P’, para α = π/
6.




O gráfico abaixo apresenta a função linear definida pelos pontos A e B, reta r .

A reta r’, simétrica de r em relação à reta e possui equação definida por:




Em um relatório, foram encontradas as seguintes matrizes:

É CORRETO afirmar que det A é igual a:
Considere as matrizes  , sendo k um número
real, com k < 2, B = (bij)
3×2, com bij = (i – j)2
, e C = A ⋅ B. Sabendo
que det C = 12, o valor de k2
é
, sendo k um número
real, com k < 2, B = (bij)
3×2, com bij = (i – j)2
, e C = A ⋅ B. Sabendo
que det C = 12, o valor de k2
é

Considere a matriz a seguir.

Assinale o conjunto de todos os valores de x reais, para os quais a matriz admite inversa.



