09da3525-bb
UECE 2014 - Matemática - Funções, Logaritmos
O maior número inteiro contido na imagem da
função real de variável real definida por
f(x) = log2(100 – x2) é
O maior número inteiro contido na imagem da
função real de variável real definida por
f(x) = log2(100 – x2) é
A
4.
B
5.
C
6.
D
7.
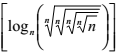 é
é
 defina, para x ≠ 0, g(x) por g(x) = log3f(x). O conjunto imagem de g, dado por
defina, para x ≠ 0, g(x) por g(x) = log3f(x). O conjunto imagem de g, dado por 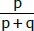 é
é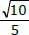
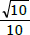
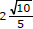
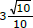
 = k podemos afirmar, corretamente, que a soma das raízes da equação 2x - 12 + 27.2 -x = 0 é igual a
= k podemos afirmar, corretamente, que a soma das raízes da equação 2x - 12 + 27.2 -x = 0 é igual a  formam, nesta ordem, uma progressão aritmética, com
formam, nesta ordem, uma progressão aritmética, com  então o valor de
então o valor de 