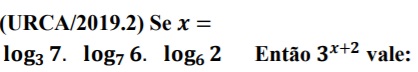Questõessobre Logaritmos
O gráfico a seguir mostra como foi o consumo de energia de uma casa ao longo dos 12 meses de um
determinado ano.

Através das informações contidas no gráfico conseguiu-se uma função definida por mais de uma sentença
que relaciona o consumo y em função do tempo x em meses, onde a e b são constantes.

Analisando a função e seu gráfico, podemos afirmar que o valor de a + b é:


O pH de uma solução é definido por 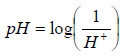 , em que H+ é a concentração
de hidrogênio em íons-grama por litro de solução.
Considerando que o suco de limão tem pH=2 ,
então a concentração de hidrogênio em íonsgrama, por litro dessa solução, é dada por
, em que H+ é a concentração
de hidrogênio em íons-grama por litro de solução.
Considerando que o suco de limão tem pH=2 ,
então a concentração de hidrogênio em íonsgrama, por litro dessa solução, é dada por
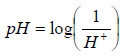 , em que H+ é a concentração
de hidrogênio em íons-grama por litro de solução.
Considerando que o suco de limão tem pH=2 ,
então a concentração de hidrogênio em íonsgrama, por litro dessa solução, é dada por
, em que H+ é a concentração
de hidrogênio em íons-grama por litro de solução.
Considerando que o suco de limão tem pH=2 ,
então a concentração de hidrogênio em íonsgrama, por litro dessa solução, é dada porO valor de mercado de um carro modelo A, daqui a t semestres é V1 = 50 000e-0,08t e o valor de
mercado de outro carro modelo B, daqui a t semestres é V2 = 50 000e-0,10t .
Após quantos semestres, contados a partir de hoje, os valores se igualarão?
Use para resolver a seguinte tabela:
x 1 2 3 4 5
ln(x) 0 0,69 1,10 1,39 1,61
Um recipiente com capacidade para 15 litros está completamente cheio de leite puro. Uma
pessoa retira 3 litros desse leite e completa o recipiente com 3 litros de água. Em seguida,
retira 3 litros dessa mistura leite/água e novamente completa o recipiente com 3 litros de água,
repetindo esse processo sucessivas vezes.Sendo k a fração da mistura final que corresponde ao leite e considerando-se, se necessário,
log 2 = 0,3, pode-se afirmar que o menor valor de n tal que k = < 1/5 é
Representar um número real x em notação científica significa escrevê-lo na forma x = p. 10q
, em
que |p|∈[1, 10[ e q é um número inteiro.
Considerando-se log2 = 0,3 e representando x = 2364 em notação científica, encontra-se o valor
de p igual a


√10
Sejam a e b números naturais para os quais log(a+1)
(b + 2a) = 2 e 1+ loga
( b - 1) = a.
Então log3a (3b - a) é igual a:
Sejam a e b números naturais para os quais log(a+1) (b + 2a) = 2 e 1+ loga ( b - 1) = a.
Então log3a (3b - a) é igual a:
A magnitude aparente de um astro de brilho B é definida a partir de uma referência B0 por meio
da fórmula  , com a seguinte convenção: “a magnitude aumenta em 5 quando o brilho
é dividido por 100”.
, com a seguinte convenção: “a magnitude aumenta em 5 quando o brilho
é dividido por 100”.
Nessas condições, considerando-se log 2 = 0,30 e log 3 = 0,48, pode-se afirmar que a magnitude
aparente da Lua, em que B = 1,2 × 105
B0, é igual a
 , com a seguinte convenção: “a magnitude aumenta em 5 quando o brilho
é dividido por 100”.
, com a seguinte convenção: “a magnitude aumenta em 5 quando o brilho
é dividido por 100”.O maior número inteiro contido na imagem da
função real de variável real definida por
f(x) = log2(100 – x2) é
Uma pesquisa realizada na primeira década do século XXI revelou que, a partir do ano
2000, em determinada região do Brasil, a expectativa de vida, em anos, sofreu modificação
e é dada pela função E(t) = 12[150 log t – 491], sendo t o ano do nascimento da pessoa.
Considerando-se log 2000 = 3,32, pode-se afirmar que uma pessoa dessa região que
tenha nascido no ano 2000, tem expectativa de viver, aproximadamente,
Um soldado fez n séries de flexões de braço, cada uma delas com 20 repetições. No entanto,
como consequência das alterações da contração muscular devidas ao acúmulo de ácido
lático, o tempo de duração de cada série, a partir da segunda, foi sempre 28% maior do que
o tempo gasto para fazer a série imediatamente anterior. A primeira série foi realizada em
25 segundos e a última em 1 minuto e 40 segundos.
Considerando log 2 = 0,3, a soma do número de repetições realizadas nas n séries é igual a:
Um soldado fez n séries de flexões de braço, cada uma delas com 20 repetições. No entanto, como consequência das alterações da contração muscular devidas ao acúmulo de ácido lático, o tempo de duração de cada série, a partir da segunda, foi sempre 28% maior do que o tempo gasto para fazer a série imediatamente anterior. A primeira série foi realizada em 25 segundos e a última em 1 minuto e 40 segundos.
Considerando log 2 = 0,3, a soma do número de repetições realizadas nas n séries é igual a:
Se α é um número real positivo tal que
Lα = 0,6933, então L ( ³√1/α.e-3) é igual a
Lx
=
logaritmo natural
de x; e é a base do
logaritmo natural.
Se y = ln(1 + sen x), para x real com x ≠ 3π/2+2kπ, k
inteiro, então temos que y’’ + e-y é igual a:
O número e é chamado de número de Euler, cujo
valor é aproximadamente e = 2,72 e ln x = loge x. Com
base nessas informações, o valor de y na equação log100
y . ln e2 = 1 é igual a:
Para medir a intensidade das ondas sonoras, costuma-se utilizar, na prática, o nível de intensidade sonora
medido em uma escala logarítmica, definida por a = 10 · log ( I/I0 ) db, em que I0 ≈ 10−12 W/m2 é a menor
intensidade do som detectável pelo ouvido humano, que corresponde ao nível zero de intensidade ou
limiar de audibilidade.
Quanto ao nível e à intensidade sonora, relacione a coluna da esquerda com a da direita.
(I) Avião próximo: a = 100 db
(II) Rua barulhenta: a = 90 db
(II) Rua barulhenta: a = 90 db
(IV) Música suave: a = 40 db
(IV) Música suave: a = 40 db
(A) I ∼ 10−10 W/m2
(B) I ∼ 10−8 W/m2
(C) I ∼ 10−6 W/m2
(D) I ∼ 10−3 W/m2
(E) I ∼ 10−2 W
m2
Assinale a alternativa que contém a associação correta.
(II) Rua barulhenta: a = 90 db
(II) Rua barulhenta: a = 90 db
(IV) Música suave: a = 40 db
(IV) Música suave: a = 40 db
(B) I ∼ 10−8 W/m2
(C) I ∼ 10−6 W/m2
(D) I ∼ 10−3 W/m2
(E) I ∼ 10−2 W m2
Um consumidor deseja adquirir um apartamento e recorre a um banco para financiar esse imóvel. Após a análise das
formas de crédito e da realização dos cálculos, o comprador opta por um financiamento no qual, ao término do prazo, o
valor total pago será igual ao dobro do valor inicial financiado.
Sabendo-se que o banco aplicou uma taxa de juros de 8% ao ano, a juros compostos, o prazo
em que esse comprador pagará seu apartamento é, em anos, igual a
Adote:
log 1,08 = 0,03
log 2 = 0,30
M = C. (1 + i) n
Em Guarapuava, a altura média de certa espécie de árvore, que se destina à produção de
madeira, é dada por h(t) = 0,8 + log2 (t+1) com h, em metros, e t, em anos.
Considerando-se que, após t anos, essa árvore atingiu 3,8m de altura, pode-se afirmar que o
valor de t é
Se
log5
x = 2
e
log10 y = 4
, então log20 y/x é
Para se calcular a intensidade luminosa L, medida em lumens, a uma profundidade de x centímetros num
determinado lago, utiliza-se a lei de Beer-Lambert, dada pela seguinte fórmula:
log (L /15 ) = −0,08x
Qual a intensidade luminosa L a uma profundidade de 12,5 cm?
Para se calcular a intensidade luminosa L, medida em lumens, a uma profundidade de x centímetros num determinado lago, utiliza-se a lei de Beer-Lambert, dada pela seguinte fórmula:
log (L /15 ) = −0,08x
Qual a intensidade luminosa L a uma profundidade de 12,5 cm?