ae6959e6-e0
FAG 2014 - Matemática - Funções, Logaritmos
A lei de resfriamento de Newton estabelece para dois corpos, A e B, com temperatura inicial de 80 °C e 160 °C,
respectivamente, imersos num meio com temperatura constante de 30 °C, que as temperaturas dos corpos, após
um tempo, t serão dadas pelas funções: TA = 30 + 50 × 10-n e TB = 30 + 130 × 10-2n onde n é uma constante.
Qual será o tempo decorrido até que os corpos tenham temperaturas iguais?
A lei de resfriamento de Newton estabelece para dois corpos, A e B, com temperatura inicial de 80 °C e 160 °C,
respectivamente, imersos num meio com temperatura constante de 30 °C, que as temperaturas dos corpos, após
um tempo, t serão dadas pelas funções: TA = 30 + 50 × 10-n e TB = 30 + 130 × 10-2n onde n é uma constante.
Qual será o tempo decorrido até que os corpos tenham temperaturas iguais?
A
(1/n) log 5
B
(1/n) log (13/5)
C
(2/n) log (18/5)
D
(2/n) log (5/2)
E
(1/n) log (2/5)


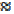
 , onde a variável
, onde a variável 











 , supondo x o maior valor inteiro possível, então, nesse caso, x
, supondo x o maior valor inteiro possível, então, nesse caso, x