Questões INSPER sobre Matemática | Pratique com o Prisma

8f3ff67f-d8

INSPER 2018 - Matemática - Aritmética e Problemas, Porcentagem

Uma das questões que mais suscita dúvidas é a diferença entre a alíquota de faixa e a alíquota efetiva do Imposto de Renda de Pessoa Física (IRPF). As alíquotas de faixa são diferentes porcentagens que são aplicadas a depender do rendimento do contribuinte. Já a alíquota efetiva refere-se ao percentual de imposto que foi efetivamente pago, ou seja, ela é obtida a partir da razão do imposto total devido pelo rendimento total do contribuinte. Os valores das duas alíquotas não coincidem por conta da metodologia de cálculo do Imposto de Renda.

A base de cálculo desse imposto é obtida pela diferença entre o total de rendimentos do contribuinte e eventuais deduções legais. Sobre o valor da base de cálculo se aplica a respectiva alíquota de faixa, e, desse resultado, é subtraída a parcela a deduzir.

Segue a tabela do IRPF vigente:

Suponha que um dado contribuinte, no último ano, tenha recebido rendimentos no valor de R$ 60.000,00 e que tenha optado por substituir todas as suas deduções legais permitidas pelo chamado modelo simplificado, que aplica um desconto de 20% sobre o total de rendimentos para a obtenção da base de cálculo. Com base nesses dados, o valor da alíquota efetiva do IRPF desse contribuinte é, aproximadamente,

A

2,5%.

B

4,6%.

C

9,7%.

D

10,1%.

E

5,3%.

8f4b477d-d8

INSPER 2018 - Matemática - Aritmética e Problemas, Porcentagem

Recentemente, uma banda internacional realizou um show no Brasil, no qual o valor arrecadado com a venda de ingressos totalizou 1,75 milhão de dólares. Esse valor arrecadado tem como destino o pagamento de impostos, o pagamento de custos fixos, e o restante é dividido entre a agência que promoveu o show e a banda que o executou.

Nesse show, o valor destinado aos custos fixos foi o triplo do valor utilizado para o pagamento de impostos. Já a agência que promoveu o show recebeu um sexto do valor destinado à banda.

Sabendo-se que o valor destinado ao pagamento de impostos e custos fixos, juntos, supera o valor destinado à agência e à banda em 770 mil dólares, o percentual do valor arrecado que foi destinado à banda é igual a

A

61%.

B

10%.

C

24%.

D

37%.

E

28%.

8f3a4333-d8

INSPER 2018 - Matemática - Sistema de Unidade de Medidas, Aritmética e Problemas, Áreas e Perímetros, Geometria Plana

Uma das áreas de testes utilizadas na pesquisa era circular, com raio igual a 100 metros. Dado que 1 hectare (ha) equivale a 10000 m2 e que a quantidade de P2 O5 aplicada foi proporcional a 50 kg por hectare, a produção de soja obtida na área em questão, segundo a fórmula apresentada, foi de, aproximadamente,

Leia o texto para responder a questão.

A deficiência de fósforo nos solos brasileiros se manifesta na baixa produtividade. Para reverter esse problema, uma equipe de agrônomos acompanhou a lavoura de um grupo de pequenos produtores, de modo a obter uma relação entre a produção S(n) de soja, em quilogramas por hectare (kg/ha), e a quantidade n de P2 O5 aplicada no solo, em kg/ha, e obteve a seguinte lei:

S(n) = 900 + 24·n – 0,05n2 , com 0 ≤ n ≤ 300

A

3100 kg.

B

31000 kg.

C

620 kg.

D

6200 kg.

E

62000 kg.

8d5045e6-d8

INSPER 2018 - Matemática - Análise de Tabelas e Gráficos

Em um estudo publicado em 2015, o Ministério da Agricultura, Pecuária e Abastecimento (MAPA) e a Empresa Brasileira de Pesquisa Agropecuária (EMBRAPA) projetaram a produção máxima de grãos no Brasil até a safra de 2024. Com uma pequena variação, de modo a simplificar os padrões apresentados, é possível retrabalhar os dados fornecidos por MAPA/ EMBRAPA referentes às safras de 2020 até 2024, conforme mostra o quadro a seguir:

Supondo que o padrão apresentado se repita até a safra de 2029, a quantidade máxima estimada de grãos, em milhões de toneladas, que será produzida em 2029 é

A

330,7.

B

341,6.

C

337,1.

D

331,7.

E

336,2.

8f2daf07-d8

INSPER 2018 - Matemática - Análise de Tabelas e Gráficos

Em 2014, a Empresa de Pesquisa Energética (EPE) publicou um estudo que apresenta análises das emissões de gases de efeito estufa (GEE) do setor de energia do Brasil no futuro. Os gráficos a seguir apresentam os dados coletados em 2014 e uma projeção para o ano de 2023.

Comparados aos dados de 2014, os dois maiores aumentos percentuais observados em 2023 são oriundos de

A

Produção/transformação de combustível e Setor de construção.

B

Transporte e Indústria.

C

Produção/transformação de combustível e Indústria.

D

Transporte e Setor de construção.

E

Setor de construção e Indústria.

8d4bfc90-d8

INSPER 2018 - Matemática - Áreas e Perímetros, Geometria Plana

Considerando que esse crescimento se repita nos próximos séculos, a área A, em milhões de quilômetros quadrados, que o Saara ocupará daqui a n anos pode ser descrita, em função de n, pela lei

Leia a notícia para responder a questão

Considerado o maior deserto quente do mundo, o Saara encontra-se em expansão. Cresceu 10% no último século e hoje ocupa uma área de quase 7400000 de quilômetros quadrados (km² ), um pouco menor que a do Brasil.

(Pesquisa Fapesp. http://revistapesquisa.fapesp.br/ 2018/05/21/saara-cresce-10-em-um-seculo. Adaptado)

A

A(n) = 7,4·0,10,01·n .

B

A(n) = 7,4·1,10,01·n

C

A(n) = 7,4·1,1n.

D

A(n) = 7,4·0,1100·n .

E

A(n) = 7,4·1,1100·n .

8d47a583-d8

INSPER 2018 - Matemática - Áreas e Perímetros, Geometria Plana

Baseando-se nos dados da notícia, é correto dizer que, um século atrás, o deserto do Saara ocupava uma área, em km² , de aproximadamente

Leia a notícia para responder a questão

Considerado o maior deserto quente do mundo, o Saara encontra-se em expansão. Cresceu 10% no último século e hoje ocupa uma área de quase 7400000 de quilômetros quadrados (km² ), um pouco menor que a do Brasil.

(Pesquisa Fapesp. http://revistapesquisa.fapesp.br/ 2018/05/21/saara-cresce-10-em-um-seculo. Adaptado)

A

6,67 · 106 .

B

6,67 · 107 .

C

6,73 · 106 .

D

6,67 · 105 .

E

6,73 · 107 .

18cd2f95-d8

INSPER 2015 - Matemática - Polígonos, Geometria Plana

O quadrilátero ABCD indicado na figura possui ângulo reto em A, um ângulo externo de 60° em B e três lados de medidas conhecidas que são AB = 7cm, BC = 6cm e C = 12cm.

Nesse quadrilátero, a medida de em centímetros, é igual a

A

3(2 + √3)

B

2(√11 + 3√3)

C

2(√11 + √3)

D

9√3

E

12√3

18d0971a-d8

INSPER 2015 - Matemática - Álgebra, Problemas

Pelas regras de um hospital:

- o turno de trabalho de cada médico deve ser de 12 horas seguidas, das 0h às 12h ou das 12h às 0h;

- na alocação de cada médico, deve haver sempre um intervalo de pelo menos 36 horas entre o término de um turno e o início de outro;

-todo médico deve ter um dia da semana fixo para folga obrigatória, no qual não pode realizar nenhum turno.

Em um mês que se inicia em uma segunda‐feira e tem 31 dias, se um médico deseja estar alocado na maior quantidade de turnos nesse hospital, ele NÃO DEVE alocar a sua folga semanal em uma

A

segunda‐feira, nem em uma quarta‐feira.

B

terça‐feira, nem em uma quarta‐feira.

C

terça‐feira, nem em uma sexta‐feira.

D

quarta‐feira, nem em um sábado.

E

sexta‐feira, nem em um domingo.

18d50ef2-d8

INSPER 2015 - Matemática - Análise Combinatória em Matemática

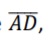
Admita que represente a soma dos números inteiros de 1 até x .Sendo assim, será igual a

A

2838.

B

2795.

C

2730.

D

1764.

E

1365.

18c8c2b5-d8

INSPER 2015 - Matemática - Análise de Tabelas e Gráficos

O salário mensal de um vendedor de carros de luxo é composto por um valor fixo de R$ 1.000,00 mais um valor de comissões sobre os carros vendidos, que custam R$ 150.000,00 cada um. O percentual de comissão inicia em 0,10% e sobe 0,02 ponto percentual para cada carro que ele consegue vender. Por exemplo, se ele vende 3 carros em um mês, sua comissão será de 0,16% por carro, sobre o preço dos carros. Dos gráficos a seguir, qual é aquele que melhor representa a relação entre o número de carros vendidos e o salário mensal do vendedor?

A

B

C

D

E

18bfb5ce-d8

INSPER 2015 - Matemática - Análise de Tabelas e Gráficos

Para que o canhão de luz possa ser posicionado apontado para o cantor em sua movimentação ao longo de toda a plataforma, o valor aproximado do ângulo α, formado pelo canhão e pelo eixo y, deve estar sempre entre

A equipe que está preparando os efeitos de iluminação de um show a ser feito em um estádio precisa instalar um canhão de luz num ponto a 20 metros de altura em relação ao chão, no qual está posicionado um palco de 20 metros de comprimento onde o cantor irá se apresentar. Para definir o ângulo de movimentação do canhão de luz de modo que ele possa acompanhar o cantor por todo o palco, a equipe modelou o problema utilizando o plano cartesiano abaixo, no qual cada unidade equivale a 10 metros.

A

18° e 27°

B

27° e 36°

C

36° e 54° .

D

54° e 63°

E

63° e 72°

18c54c8a-d8

INSPER 2015 - Matemática - Áreas e Perímetros, Geometria Plana

Para que não seja formada nenhuma sombra na projeção de luz feita pelo canhão, não pode haver nenhum objeto posicionado no espaço indicado pela região sombreada na figura, cuja área é igual a

A equipe que está preparando os efeitos de iluminação de um show a ser feito em um estádio precisa instalar um canhão de luz num ponto a 20 metros de altura em relação ao chão, no qual está posicionado um palco de 20 metros de comprimento onde o cantor irá se apresentar. Para definir o ângulo de movimentação do canhão de luz de modo que ele possa acompanhar o cantor por todo o palco, a equipe modelou o problema utilizando o plano cartesiano abaixo, no qual cada unidade equivale a 10 metros.

A

2 m2 .

B

4 m2 .

C

20 m2 .

D

40 m2 .

E

200 m2 .

18bb45df-d8

INSPER 2015 - Matemática - Funções, Função de 1º Grau

Uma companhia aérea começa a vender bilhetes para os voos de um dia específico com antecedência de um ano. O preço p(t), em reais, que ela cobra por um determinado trecho vai aumentando conforme se aproxima a data do voo, de acordo com a lei
p(t) = 200 - 4t,
em que t é o tempo, em dias, que falta para a respectiva data.
Considere que a quantidade vendida v em cada um desses dias varia em função do preço p(t) e do tempo t, segundo a expressão
v = 0,0002 . t . p(t)
O valor arrecadado por essa companhia no dia em que a quantidade vendida é máxima é igual a

A

R$ 30.000,00.

B

R$ 40.000,00.

C

R$ 50.000,00.

D

R$ 60.000,00.

E

R$ 70.000,00.

18b39838-d8

INSPER 2015 - Matemática - Aritmética e Problemas, Porcentagem

Se o salário atual dos trabalhadores é de R$2.000,00, o aumento total pleiteado por eles, incluindo o reajuste da cesta básica, será de, aproximadamente,

Funcionários de obras para Olimpíada 2016 entram em greve no Rio

18/05/2015 às 20h23

    RIO ‐ Funcionários das principais obras para a Olimpíada de 2016, no Rio, entraram em greve nesta segunda‐feira. (...)
    "Decidimos iniciar a greve (...) e caso não ocorra um acordo ficaremos parados por tempo indeterminado.", declarou o diretor do sindicato.
    Ele ainda afirmou que a paralisação por um tempo maior pode gerar problemas na entrega das obras. "Caso não haja acordo, a greve pode afetar os prazos de entrega. Isso ainda pode gerar até um custo maior para as empresas como ocorreu na reforma do Maracanã para a Copa do Mundo, onde na fase final tiveram que dobrar o número de funcionários para concluir a obra.”
    Entre as reivindicações dos trabalhadores estão o aumento no valor da cesta básica de R$ 310 para R$ 350 e um reajuste no valor do salário de 8,5%.
    (...) Renilda Cavalcante, que representa as empresas responsáveis pelas obras, afirma que a adesão à greve foi de cerca de 30%.

Adaptado de: http://www.valor.com.br/brasil/4055142/funcionarios‐de‐ obras‐para‐olimpiada‐2016‐entram‐em‐greve‐no‐rio.

A

8%.

B

9%.

C

10%.

D

11%.

E

12%.

18b7dc3a-d8

INSPER 2015 - Matemática - Aritmética e Problemas, Porcentagem

Considere que:

-T é o tempo que resta para a obra ser concluída, a partir do início da greve;

-p é o percentual, em relação a T correspondente ao tempo que durar a greve;

-a partir do momento em que a greve terminar, serão contratados funcionários adicionais suficientes para que a obra seja finalizada dentro do prazo, para trabalharem em todo período restante;

-a produtividade de cada trabalhador na ativa é sempre a mesma, independentemente do período.

Para que o impacto no período subsequente ao fim da greve seja o mesmo da reforma do Maracanã, o valor de p deve ser aproximadamente igual a

Funcionários de obras para Olimpíada 2016 entram em greve no Rio

18/05/2015 às 20h23

    RIO ‐ Funcionários das principais obras para a Olimpíada de 2016, no Rio, entraram em greve nesta segunda‐feira. (...)
    "Decidimos iniciar a greve (...) e caso não ocorra um acordo ficaremos parados por tempo indeterminado.", declarou o diretor do sindicato.
    Ele ainda afirmou que a paralisação por um tempo maior pode gerar problemas na entrega das obras. "Caso não haja acordo, a greve pode afetar os prazos de entrega. Isso ainda pode gerar até um custo maior para as empresas como ocorreu na reforma do Maracanã para a Copa do Mundo, onde na fase final tiveram que dobrar o número de funcionários para concluir a obra.”
    Entre as reivindicações dos trabalhadores estão o aumento no valor da cesta básica de R$ 310 para R$ 350 e um reajuste no valor do salário de 8,5%.
    (...) Renilda Cavalcante, que representa as empresas responsáveis pelas obras, afirma que a adesão à greve foi de cerca de 30%.

Adaptado de: http://www.valor.com.br/brasil/4055142/funcionarios‐de‐ obras‐para‐olimpiada‐2016‐entram‐em‐greve‐no‐rio.

A

44%.

B

55%.

C

66%.

D

77%.

E

88%.

18af5764-d8

INSPER 2015 - Matemática - Probabilidade

Uma floricultura recebe as flores que comercializa de seus fornecedores na forma de brotos que ainda não floresceram. Esses brotos levam de 3 a 8 dias para começar a desabrochar e, quando iniciam, levam de 2 a 7 dias para abrir totalmente. As flores permanecem um dia totalmente abertas e depois começam a perder pétalas, ficando feias para serem vendidas. Por mais que os floristas tenham experiência, não lhes é possível prever quantos dias um broto levará para começar a desabrochar, pois isso pode ocorrer com igual probabilidade em qualquer um dos dias desse período; e o tempo para abrir totalmente é igualmente imprevisível e independente do período anterior. A floricultura precisará fazer a decoração para um casamento, com uma grande quantidade de flores, que precisam estar totalmente abertas no dia da celebração. Qual a antecedência mais adequada para que a floricultura receba um grande lote de flores de seus fornecedores, de modo a ter a maior quantidade de flores deste lote que estejam conforme a exigência estabelecida?

A

5 dias.

B

8 dias.

C

10 dias.

D

12 dias.

E

15 dias.

18a4df7c-d8

INSPER 2015 - Matemática - Funções, Função de 1º Grau

No plano cartesiano 0xy ,equações lineares com duas incógnitas, do tipo ax + by = c representam retas. Já em relação a um sistema de coordenadas cartesianas 0xyz no espaço, equações lineares com três incógnitas representam planos. Por exemplo, na figura ao lado, pode‐se ver a representação da equação 2x + y + z = 4 em relação ao sistema de coordenadas 0xyz

A solução gráfica de um sistema de equações lineares 3 X 3 é a região do espaço correspondente à intersecção dos planos definidos pelas três equações lineares que compõem o sistema. Sendo assim, das representações gráficas numeradas ao lado, correspondem a sistemas lineares 3 X 3 com infinitas soluções apenas

A

5, 7 e 8.

B

1, 3 e 7.

C

4, 6 e 8.

D

2, 5 e 7.

E

1, 2, 3, 5 e 7

18a80e1f-d8

INSPER 2015 - Matemática - Aritmética e Problemas, Razão, Proporção e Números Proporcionais

No tratamento de uma infecção contraída simultaneamente por dois irmãos, o médico passou para os pais das crianças a receita ao lado. Se o mais novo pesa 20 quilogramas e o mais velho pesa 30 quilogramas, então as dosagens que eles devem receber em cada aplicação são,respectivamente, de

A

30 e 40 gotas.

B

35 e 45 gotas.

C

35 e 40 gotas.

D

30 e 45 gotas.

E

40 e 45 gotas.

18ac248a-d8