Em muitos países, o clima econômico melhorou desde os primeiros dias da crise financeira de 2009. O gráfico a seguir
mostra um comparativo do percentual da população de cinco
países que avalia como boa a situação econômica de seu
país
em 2009 e 2018.
(www.pewresearch.org. Adaptado.)
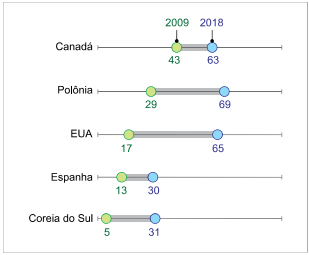
Os países que apresentaram a maior e a menor variação no
percentual da população que avalia como boa a situação econômica de seu país no período analisado são, respectivamente,
Em muitos países, o clima econômico melhorou desde os primeiros dias da crise financeira de 2009. O gráfico a seguir mostra um comparativo do percentual da população de cinco países que avalia como boa a situação econômica de seu país em 2009 e 2018.

(www.pewresearch.org. Adaptado.)
Os países que apresentaram a maior e a menor variação no
percentual da população que avalia como boa a situação econômica de seu país no período analisado são, respectivamente,



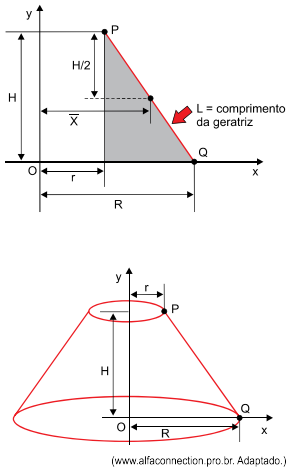
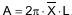 , sendo
que as medidas utilizadas na fórmula se relacionam com as
medidas do tronco, conforme mostra o esquema.
, sendo
que as medidas utilizadas na fórmula se relacionam com as
medidas do tronco, conforme mostra o esquema.