Em um jogo, temos um tabuleiro como o da imagem abaixo e três jogadores. Cada jogador deverá
posicionar uma peça no centro de cada um dos espaços numerados, não podendo haver peças de
dois jogadores em um mesmo espaço. A cada rodada, são rolados dois dados de seis faces e somamse os resultados obtidos em cada dado. A partir dessa soma, todos os espaços que contém o número
obtido podem produzir a matéria prima indicada. Por exemplo, se a soma dos dados for o número 2, o
jogador com sua peça posicionada no espaço de número dois, produzirá madeira.
O primeiro jogador deseja ter a maior chance possível de obter madeira; o segundo, a maior chance
possível de obter trigo; e o terceiro, a maior chance possível de obter minério.
Analise as afirmativas.
I - O primeiro jogador deve posicionar sua peça no espaço de número 7.
II - O primeiro jogador deve posicionar sua peça no espaço de número 8.
III - O segundo jogador deve posicionar sua peça no espaço de número 12.
IV - O segundo jogador pode escolher tanto o espaço de número 6 como o de número 8.
V - O terceiro jogador deve posicionar sua peça no espaço de número 6.
Assinale a alternativa que contém a(as) afirmativa(s) correta(s).
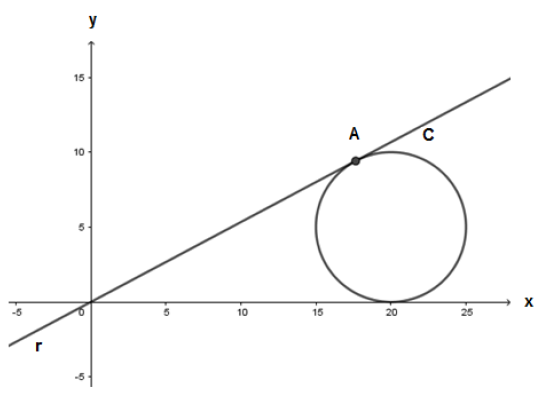

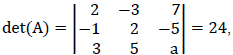 o det(2A) é
o det(2A) é



