Questõesde IF-RS sobre Matemática

InícioTodas as questões
1
1
Foram encontradas 42 questões
65298b27-d9
IF-RS 2018 - Matemática - Números Complexos

Considere as afirmações abaixo.


I - x2 ≥ x, para todo número real x.

II- -2x-6/x-12 ≥ 0, para todo x número real no intervalo [2, 11].

III- √x2 + 2x + 1 = x + 1, para todo número real x.


Assinale a alternativa correta.

A
É verdadeira somente a afirmação I.
B
É verdadeira somente a afirmação II.
C
É verdadeira somente a afirmação III.
D
São verdadeiras somente as afirmações I e II.
E
São verdadeiras somente as afirmações II e III.
65220651-d9
IF-RS 2018 - Matemática - Progressão Aritmética - PA, Geometria Plana, Triângulos, Progressões

Na figura abaixo, temos uma sequência de triângulos, todos de base a. A altura do primeiro triângulo é h e as medidas das alturas dos triângulos estão em progressão aritmética de razão p.



É correto afirmar que as sequências das áreas dos triângulos formam uma

A
progressão aritmética de razão ap/2.
B
progressão aritmética de razão p.
C
progressão geométrica de razão p.
D
progressão geométrica de razão ap/2.
E
sequência numérica que não é uma progressão aritmética nem geométrica.
6525510c-d9
IF-RS 2018 - Matemática - Pontos e Retas, Circunferências e Círculos, Geometria Analítica, Geometria Plana

Na figura abaixo, o ângulo  mede π/6 radianos, e o ponto é o centro da circunferência de raio 3. A área do triângulo ABC, em unidades de área, é 


A
√3/2
B
√3
C
√11
D
9/2
E
2√6
65317d72-d9
IF-RS 2018 - Matemática - Aritmética e Problemas, Médias

Uma farmácia vende em média 1.050 remédios por mês. O preço médio dos medicamentos dessa farmácia é de R$ 80,00. Para aumentar seu faturamento médio, o gerente pretende dar um desconto de R$ 1,00 no preço médio dos medicamentos. Assim, 105 medicamentos serão vendidos a mais por mês. Nesse caso, qual é o preço médio dos medicamentos, em reais, que vai maximizar o faturamento da farmácia?

A
80,00
B
70,00
C
45,00
D
40,00
E
35,00
6514cc35-d9
IF-RS 2018 - Matemática - Áreas e Perímetros, Geometria Plana

A prefeitura de uma cidade pretende fazer um pequeno espaço de convivência em um terreno retangular com medidas de 20 metros por y metros. Para isso, será necessário plantar grama no pentágono HGFBE, conforme figura abaixo. O valor de y, em metros, para que a área de grama a ser plantada seja de 180 m2 , é


A
18
B
15
C
10
D
7,5
E
5
651975cb-d9
IF-RS 2018 - Matemática - Probabilidade

Em um jogo com 15 cartas, sendo uma delas a cartão do Dragão, antes do início da partida, os jogadores devem embaralhá-las e sortear apenas 5 para fazerem parte do jogo. A probabilidade da carta do Dragão fazer parte de uma partida deste jogo é

A
1/15
B
1/5
C
1/3
D
2/3
E
4/5
651e7591-d9
IF-RS 2018 - Matemática - Probabilidade

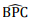
Em uma caixa, existem só bolas numeradas de um a dez. Supondo que todas as bolas têm a mesma probabilidade de serem retiradas da caixa e sabendo que a probabilidade de retirar uma bola com o número n é de (1/2)n para cada . Qual a probabilidade de se retirar uma bola com o número dez?

A
1/2
B
1/4
C
(1/2)8
D
(1/2)9
E
(1/2)10
65114681-d9
IF-RS 2018 - Matemática - Funções, Equações Exponenciais

Sabendo que f (x) = 2x e g (x) = 2-x , considere as afirmações abaixo.


I - f (x) + g (x) ≥ 2, para todo número real.

II - f (x) + g (x) = f (-x) + g (-x), para todo x número real.

III - se x > y então g (x) > g (y).


Assinale a alternativa correta.

A
É verdadeira somente a afirmação I.
B
É verdadeira somente a afirmação II.
C
São verdadeiras somente as afirmações I e II.
D
São verdadeiras somente as afirmações I e III.
E
São verdadeiras somente as afirmações II e III.
87e54f6e-b6
IF-RS 2017 - Matemática - Pontos e Retas, Geometria Analítica

A equação da reta que passa pelos pontos A(0,2) e B(2, -2) é

A
y = 2x + 2
B
y = -2x -2
C
y = x
D
y = -x +2
E
y = -2x + 2
87e0725e-b6
IF-RS 2017 - Matemática - Sistema de Unidade de Medidas, Aritmética e Problemas

O raio da circunferência inscrita na base de um cubo é 2cm. Esse cubo, em um primeiro momento, está com água até a metade de sua altura; em seguida é adicionada uma quantidade de água fazendo com que a coluna de água no cubo suba até 3/4 da altura total.

O volume de água adicionado a mais ao cubo, em cm³ , é

A
4
B
8
C
16
D
32
E
48
87d283d6-b6
IF-RS 2017 - Matemática - Áreas e Perímetros, Geometria Plana

Na figura abaixo, temos uma sequência de retângulos, todos de altura a. A base do primeiro retângulo é b e dos retângulos subsequentes é o valor da base do anterior mais uma unidade de medida. Sendo assim, a base do segundo retângulo é b+1 e do terceiro b+2 e assim sucessivamente.


Considere as afirmativas abaixo.

I - A sequência das áreas dos retângulos é uma progressão aritmética de razão 1.

II - A sequência das áreas dos retângulos é uma progressão aritmética de razão a.

III - A sequência das áreas dos retângulos é uma progressão geométrica de razão a.

IV - A área do enésimo retângulo (An) pode ser obtida pela fórmula An = a . (b + n -1).


Assinale a alternativa que contém a(as) afirmativa(s) correta(s).

A
I.
B
II.
C
III.
D
II e IV.
E
III e IV.
87cea1aa-b6
IF-RS 2017 - Matemática - Análise de Tabelas e Gráficos, Funções, Função de 2º Grau

O gráfico abaixo representa a função f(x) = a + b.sen(x) .



Nessas condições, é correto afirmar que

A
a = -2 e b = 1
B
a = -1 e b = 2
C
a = 1 e b = -1
D
a = 1 e b = -2
E
a = 2 e b = -1
87ca0122-b6
IF-RS 2017 - Matemática - Funções, Equações Exponenciais

O crescimento de uma colônia de bactérias é determinado pela função: Q(t) = Qo . 3t .
Sendo Qo a quantidade inicial de bactérias na colônia e  t  o tempo decorrido em horas, quanto tempo a quantidade de bactérias será 9 vezes maior que a quantidade inicial?

A
1 h
B
1 h e 30 min.
C
2 h.
D
3 h
E
9 h.
87c546bc-b6
IF-RS 2017 - Matemática - Funções, Função de 1º Grau

O preço cobrado por uma corrida de taxi é constituído por um valor inicial fixo, a bandeirada, e acrescido de um valor por quilômetro rodado. O preço da bandeirada é R$ 5,18 e do quilômetro rodado R$ 2,59. A função f(x) que calcula o valor de uma viagem, onde x é a quantidade de quilômetros rodados na corrida, nessas condições é

A
f(x) = 2,59x+ 5,18
B
f(x) = 5,18x + 2,59
C
f(x) = 7,77x
D
f(x) = 2,59 + 7,77x
E
f(x) = 5,18 + 7,77x
87bbe102-b6
IF-RS 2017 - Matemática - Análise de Tabelas e Gráficos

O gráfico abaixo apresenta a variação do custo do kWh no Rio Grande do Sul de três concessionárias diferentes de 2010 até 2015. A partir desse gráfico, podemos observar o comportamento da tarifa de energia elétrica ao longo dos anos em cada uma das três concessionárias.



Com base no gráfico podemos afirmar que

I - de 2010 até 2012, a concessionária C possuía o maior preço do kWh e, em 2013, sofreu uma redução e passou a não ter mais o maior custo entre as três concessionárias.
II - do ano de 2014 para o ano de 2015, a concessionária B teve a maior variação percentual no valor do kWh dentre as três concessionárias.
III - o valor do kWh ao longo desses anos apresentou um crescimento constante.
IV - comparando os anos de 2010 e 2014, apenas uma concessionária apresentou preço menor em 2014 do que em 2010.

Quais afirmações estão corretas?

A
Apenas I e II.
B
Apenas I, II e III.
C
Apenas I, II e IV.
D
Apenas II e IV.
E
I, II, III e IV.
dab414b3-c1
IF-RS 2017 - Matemática - Seno, Cosseno e Tangente, Trigonometria

Dada a circunferência C : ( x-20)2 + (y-5)2 = 25, a equação da reta r, que contém a origem e é tangente à circunferência C no ponto A, conforme figura abaixo, é

A

y = 1/2 x

B

y = 8/15 x

C

y = 9/17 x

D

y = 2x

E

y = 1/2 x + 1

dab00b27-c1
IF-RS 2017 - Matemática - Áreas e Perímetros, Progressão Aritmética - PA, Geometria Plana, Progressões

Considere uma sequência de quadrados em que o primeiro tem área 1, o segundo tem área 2 e assim sucessivamente. Sabendo que as medidas das diagonais destes quadrados estão em progressão aritmética, a área do vigésimo quadrado em u.a., é

A

√40

B
10
C
38-18√2
D
20
E

daac9031-c1
IF-RS 2017 - Matemática - Pontos e Retas, Geometria Analítica

Duas cordas são amarradas no topo de um poste perpendicular ao solo. Estas cordas são fixadas no solo esticadas e fazendo ângulos de com o solo. Sabendo que o poste tem 5 metros de altura, uma das cordas foi fixada no solo a uma distância de

A
7 metros do poste.
B
10 metros do poste.
C
5 metros do topo do poste.
D
10 metros do topo do poste.
E
12 metros do topo do poste.
daa2a343-c1
IF-RS 2017 - Matemática - Matrizes, Álgebra Linear

Sabendo que o

A

24

B
48
C
106
D
192
E
212
daa887f5-c1
IF-RS 2017 - Matemática - Álgebra Linear - Equações Lineares, Espaço Vetorial e Transformações Lineares e Matrizes, Álgebra Linear

Em uma partida de vôlei, um jogador dá um saque. Em cada instante de tempo t, para tpertence[0,10], a bola tem altura h(t) = -t² + 10t + 1,6.


Considere as afirmações abaixo.


I - Se este saque ocorresse em um ginásio com teto de 30m de altura, a bola alcançaria o teto.

II - A bola alcança a altura máxima no instante t = 5.

III - Se este saque ocorresse em um ginásio com teto de 17,6m de altura, a bola alcançaria o teto no instante t = 2.

A
I.
B
II.
C
I e II.
D
I e III.
E
II e III.