Questõesde IF-PR sobre Matemática

InícioTodas as questões
1
1
Foram encontradas 489 questões
f06bcc9c-f9
IF-PR 2019 - Matemática - Aritmética e Problemas, Razão, Proporção e Números Proporcionais, Médias

A tabela seguinte fornece o número de peças defeituosas por peças confeccionadas em uma determinada fábrica.


A razão entre a média das peças confeccionadas e a média das peças defeituosas é igual a:

A
5.
B
10.
C
15.
D
25.
f068ddd8-f9
IF-PR 2019 - Matemática - Geometria Plana, Ângulos - Lei Angular de Thales, Triângulos

Uma pessoa está a uma distância d = 300 cm de uma parede e, com uma caneta laser, aponta para a mesma sob um ângulo α = π/ 6 em uma trajetória retilínea, marcando a altura h. Apontando para a mesma parede, sob um ângulo 2α, atinge a parede a uma altura sob um ângulo H. A diferença entre as alturas é, em cm:

A
150.
B
200√3
C

D

f06529b4-f9
IF-PR 2019 - Matemática - Circunferências e Círculos, Geometria Plana

Infinitas circunferências são concêntricas, de raios r1 , r2 , r 3 , …, com . Sabendo que r1 = 1 cm, a soma do comprimento de todas as circunferências é, em cm, igual a:

A
(2π)∞
B
(1/2)∞
C
4π
D
1
f062067b-f9
IF-PR 2019 - Matemática - Funções, Função de 1º Grau

A função L(t) = 2000 x (1,5)t representa o lucro mensal de uma empresa. O lucro dessa empresa, após 3 meses, em reais, será de:

A
9000.
B
8750.
C
7500.
D
6750.
f056294e-f9
IF-PR 2019 - Matemática - Matrizes, Álgebra Linear

O gráfico abaixo apresenta a função linear definida pelos pontos A e B, reta r .

A reta r’, simétrica de r em relação à reta e possui equação definida por:





A

B

C

D

f05e7e8d-f9
IF-PR 2019 - Matemática - Matrizes, Álgebra Linear

As coordenadas de um ponto P, no plano cartesiano, são (a,b) = (1,1). é uma matriz de rotação, P’ = M × P. Assinale a alternativa que apresenta as coordenadas de P’, para α = π/ 6.

A

B

C

D

f0527649-f9
IF-PR 2019 - Matemática - Áreas e Perímetros, Geometria Plana

O tangran tem várias formas, sendo uma delas o formato de coração, composto de semicírculo, triângulo retângulo isósceles, quadrado e paralelogramo. Na figura, as "marquinhas" sobre os segmentos indicam que eles são congruentes, de medida x = 10 cm.

Sabendo-se que π = 3,14, pode-se afirmar que a área do trangran é, em cm2 , igual a:

A
714.
B
257.
C
478,5.
D
414,28.
f04f50a6-f9
IF-PR 2019 - Matemática - Funções, Função de 2º Grau

Transladando a função y1 (x) = x2 obtém-se y2 (x) = (x–2)2 . E, transladando y2 (x), resulta na função y3 (x) = (x–2)2 – 2. Em relação às funções, é correto afirmar que:

A
y1 e y2 possuem dois pontos em comum.
B
y2 e y3 possuem pontos em comum.
C
y2 (x) > y3 (x),para tudox ∈ reto números reais.
D
y1 (x) = y3 (x), para tudox ∈ reto números reais.
f05a48d3-f9
IF-PR 2019 - Matemática - Álgebra Linear, Sistemas Lineares

Considere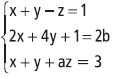 , sendo a e b números reais.

O sistema linear tem solução única, se:

A
a ≠ –1
B
b ≠ –1
C
a = –1 e b = –4
D
a = –1 e b ≠ –4
f04c4531-f9
IF-PR 2019 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

Em uma determinada região litorânea, a maré oscila segundo a função h(t) = 3 – 2sen( πt/ 12 ), sendo h a altura em metros, que a maré atinge no tempo t em horas, medido a partir de 6h da manhã. Uma embarcação, que se encontra encalhada às 11h da manhã, precisa de uma profundidade mínima de 2 metros para navegar. Assinale a alternativa que apresenta quantas horas os tripulantes dessa embarcação ainda terão que esperar para prosseguirem viagem.

A
4h.
B
5h.
C
6h.
D
7h.
f0487dab-f9
IF-PR 2019 - Matemática - Sistema de Unidade de Medidas, Aritmética e Problemas, Geometria Espacial, Cilindro

Uma cisterna subterrânea para captação de água da chuva é composta por três partes, como mostra a figura abaixo. A e C são semiesferas equivalentes e B é um cilindro. Sabendo que 1dm3 = 1l.


Considerando a constante π igual a 22/7 , a capacidade da cisterna é, em litros, de aproximadamente:

A
140.
B
7300.
C
1430.
D
750.
abf66901-b3
IF-PR 2016 - Matemática - Progressão Geométrica - PG, Progressões

Encontre o primeiro termo de uma progressão geométrica decrescente e ilimitada, de razão igual a 1/2 , sabendo que o limite da soma dos seus termos é igual a 16.

A
16.
B
32.
C
8.
D
64.
abf27cd0-b3
IF-PR 2016 - Matemática - Álgebra Linear, Sistemas Lineares

Encontre todos os valores de a e b , para que o sistema de equações abaixo seja impossível.


A
a = 7 e b ≠ –10.
B
a = 7 e b = –10.
C
a = –7 e b ≠ 10.
D
a ≠ – 7 e b ≠ –10.
abee99dc-b3
IF-PR 2016 - Matemática - Matrizes, Álgebra Linear

Considere a matriz a seguir.


Assinale o conjunto de todos os valores de x reais, para os quais a matriz admite inversa.

A

B

C

D

abe9f15d-b3
IF-PR 2016 - Matemática - Matrizes, Álgebra Linear

Seja A uma matriz quadrada de elementos reais, com exatamente 3 linhas e 3 colunas. Se o determinante de A é igual a 5, então calcule o valor do determinante da matriz dada por: 2.A.AT.A–1, onde AT e A–1, representam a matriz transposta e a matriz inversa de A, respectivamente.

A
20.
B
40.
C
60.
D
80.
abd87ccd-b3
IF-PR 2016 - Matemática - Aritmética e Problemas, Médias

Durante 150 semanas o supervisor de uma fábrica observou o número de peças com defeito descartadas, apresentadas na planilha abaixo.


A média do número de peças descartadas por apresentar defeito, por semana, é de:

A
1,87.
B
1,5.
C
0,76.
D
0,53.
abe5998d-b3
IF-PR 2016 - Matemática - Funções, Logaritmos

Considerando que log10 2 = α e que log10 3 = β, calcule o valor de log9 5

A


B

C

D

abe20137-b3
IF-PR 2016 - Matemática - Análise de Tabelas e Gráficos

No Campeonato Grandes Marcas são avaliados os desempenhos dos carros em uma corrida e receberão pontuação de acordo com a posição ao final da corrida de cada temporada como mostra a tabela abaixo.


Se o gráfico apresenta o desempenho da marca Velox-Dade, a pontuação total é igual a:


A
14.
B
22.
C
43.
D
73.
abdcd13c-b3
IF-PR 2016 - Matemática - Funções, Equações Exponenciais

Encontre o domínio natural da função 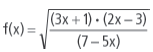(isto é, encontre todos os valores reais de x, para os quais

A

B

C

D

abd53b70-b3
IF-PR 2016 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

Sendo x e a, números reais tais que 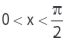e sec x = a – 1, então tg2 x é igual a:

A
a(a – 2).
B
a(a – 1).
C
a2.
D
1 – a2 .