Questõesde UEG sobre Geometria Plana

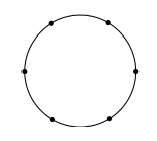
Na figura a seguir tem-se um círculo inscrito em um hexágono, que está inscrito em outro círculo.

O raio do círculo maior R em função do raio do círculo menor r pode ser representado pela função

Na figura a seguir, a reta que passa pelos pontos A e B possui equação y = 2x - 1, ao passo que a reta que contém o ponto B e C é y = -2x + 11.

Dessa forma, a altura h na figura é

Um edifício de 4 andares possui 4 apartamentos por andar, sendo que em cada andar 2 apartamentos possuem 60 m² e 2 apartamentos possuem 80 m². O gasto mensal com a administração do edifício é de R$ 6.720,00. Sabendo-se que a cota de condomínio deve ser dividida proporcionalmente à área de cada apartamento, logo quem possui um apartamento de 80 m² deve pagar uma cota de

Na figura a seguir tem-se que .

A área do triângulo DGH destacado pode ser dada pela expressão:

Uma laranja com formato esférico e com 6 cm de diâmetro foi descascada até a sua metade. Considerando-se esses dados, verifica-se que a área total da casca retirada da laranja é de aproximadamente (use π = 3,14)

Observe a figura a seguir.

Sabendo-se que a circunferência de maior raio passa pelo centro da circunferência de menor raio, a equação da circunferência de maior raio é

Uma circunferência com centro na origem está tangenciando duas retas paralelas de equações y = -2x + b e y = -2x + c . Nesse caso, o valor de b + c é

Observando-se o desenho a seguir, no qual o círculo tem raio r, e calculando-se o apótema a4, obtemos

Duas circunferências possuem equações ( x+1)2 + y2 = 1 e (x-1)2 + y2 = 1. A intersecção entre as duas circunferências

Um triângulo equilátero está inscrito em uma circunferência centrada na origem e um dos seus vértices é o ponto (2,0). Os outros vértices do triângulo são os pontos

Na figura a seguir, AD mede 12 cm, BD mede 4 cm, BC mede 12 cm, o ângulo B mede 90º e DE é paralelo a BC.

Ao rotacionarmos o trapézio BCED em torno do lado BD, produzimos um tronco de cone cujo volume é

Em um plano inclinado, que faz um ângulo θ com a horizontal, é colocado um corpo de massa m, preso a uma mola de constante elástica k, que provoca uma deformação x na mola. O sistema está em equilíbrio e existe atrito entre o plano inclinado e o corpo, cujo coeficiente de atrito é dado por μ. Nessa situação, a expressão que representa a constante elástica da mola é

A melhor maneira de alocarmos pontos igualmente espaçados em um círculo é escrevê-los nos vértices de polígonos regulares, conforme a figura a seguir exemplifica com 6 pontos.

Para alocarmos 36 pontos igualmente espaçados em um círculo de raio 1, a distância mínima entre eles deve ser aproximadamente

use sen(5°)= 0,08

As ações de uma empresa variaram semanalmente conforme os dados da figura a seguir.

De acordo com os dados apresentados, o período de maior variação ocorreu entre as semanas

Ao girarmos um quadrado ABCD de lado igual a 3 em torno do vértice A, mantendo-o fixo, os vértices B e C descrevem circunferências concêntricas com centro em A. A área do anel circular entre essas duas circunferências é

Na aula de matemática, a professora mostrou um sólido no formato de uma pirâmide hexagonal regular, cuja aresta da base media l = 4 cm e a área lateral da pirâmide era de 60 cm2 . Em seguida, solicitou aos alunos que calculassem o volume dessa pirâmide. O valor encontrado foi de

Um triângulo isósceles possui um vértice no ponto (3,5) e a base sobre a reta y = -1. A altura desse triângulo é igual a

Ao planificarmos um cilindro circular reto cuja altura é igual a 6 cm e cujo raio da base é igual a 4 cm, obtemos uma figura plana cuja área é aproximadamente igual a