Questõesde UEFS sobre Geometria Plana

InícioTodas as questões
1
1
1
Foram encontradas 38 questões
c8282af0-e8
UEFS 2011 - Matemática - Circunferências e Círculos, Geometria Plana

Considere, no sistema de coordenadas cartesianas, uma circunferência que tangencia o eixo das ordenadas em y= √112 e também tangencia a reta √7y - 3x =0.

Sabendo-se que nenhum ponto da circunferência tem coordenadas negativas, pode-se afirmar que a distância do centro da circunferência à origem é, em u.c., aproximadamente, igual a

A
8
B
9
C
10
D
11
E
12
c81aea1a-e8
UEFS 2011 - Matemática - Áreas e Perímetros, Geometria Plana

O quadrado e o círculo representados na figura têm centro no mesmo ponto e, nessa figura, as regiões sombreadas têm área de mesma medida.



Nessas condições, pode-se afirmar que

A
a área do círculo é menor do que a área do quadrado.
B
a área do círculo é menor do que a área do quadrado.
C
a área do círculo é maior do que a área do quadrado.
D
a relação entre as áreas do círculo e do quadrado depende da medida do lado do quadrado.
E
a relação entre as áreas do círculo e do quadrado depende da medida do raio da circunferência.
c815acb4-e8
UEFS 2011 - Matemática - Geometria Plana, Triângulos



O triângulo QRN, na figura, foi obtido, girando-se o triângulo MNO em torno do ponto N. Sabendo-se que MNQ = 90°, NQR = 42°, NRQ = 78° e, considerando-se P o ponto de intersecção dos segmentos OR e QN, pode-se afirmar que o ângulo OPN mede

A
95º
B
99º
C
102º
D
105º
E
108º
c80bd8b2-e8
UEFS 2011 - Matemática - Geometria Plana, Triângulos



Estudos mostraram a viabilidade da construção de uma ponte ligando uma cidade litorânea a uma ilha, a partir de um ponto P ou de um ponto Q da costa, distantes 2400m um do outro, até um ponto I da referida ilha.

Sabe-se que se a ponte for construída a partir de P ou de Q, formará com PQ ângulos de 45º e 60º, respectivamente, e que, nas duas situações, o custo de construção é de 100 unidades monetárias por metro linear.

Com base nessas informações e considerando-se sen 75º = 0,96, √2 = 1,4 e √3 = 1,7 , pode-se afirmar que, optando-se pela construção da ponte menor, haverá uma economia, em unidades monetárias, de

A
12500
B
20350
C
37500
D
41330
E
51200
c7e16bd8-e8
UEFS 2011 - Matemática - Circunferências e Círculos, Geometria Plana

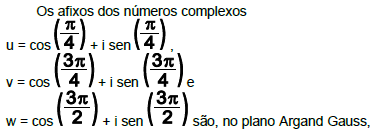
Considerem-se, no plano complexo representado na figura, os pontos P, Q e R pertencentes a uma circunferência de centro na origem.



Sendo P o afixo de z = 2 - 3/2 i e QR, um arco medindo 5π/12 u.c, pode-se afirmar que o ponto R é afixo do número complexo que pode ser representado, algebricamente, por

A
5/4 (-1 + i √3)
B
5√2/4 (-1 + i √3)
C
5/4 (-√3 + i)
D
7/4 (-√3 + i)
E
5√2/4 (-1 + i )
0cb2b730-e7
UEFS 2009 - Matemática - Circunferências e Círculos, Polígonos, Geometria Plana



A porta de uma sala quadrada cujo lado mede 4m, tem 0,80m de largura, está posicionada a 0,50m de um dos cantos, de acordo com a figura, e quando aberta para o interior da sala, tangencia no ponto T, um tapete circular colocado no centro da sala.

Com base nessa informação, pode-se afirmar que o diâmetro do tapete mede

A
2,2m
B
2,6m
C
3,0m
D
3,4m
E
3,8m
0cadf073-e7
UEFS 2009 - Matemática - Áreas e Perímetros, Pontos e Retas, Geometria Analítica, Geometria Plana

A área da região limitada pelos eixos cartesianos coordenados pela reta r de equação 2y – x – 2 = 0 e pela reta s, perpendicular a r e que passa pelo ponto P = (2, 2), mede, em u.a.,

A
2,5
B
3,4
C
4,0
D
5,8
E
7,0
0c6e2d4f-e7
UEFS 2009 - Matemática - Circunferências e Círculos, Geometria Plana

A
pontos colineares.
B
vértices de um triângulo equilátero.
C
vértices de um triângulo retângulo.
D
pontos de uma circunferência com centro na origem e raio 1.
E
pontos de uma circunferência com centro na origem e raio √ 2.
e5bd29c6-e7
UEFS 2010 - Matemática - Circunferências e Círculos, Geometria Plana

Considerando-se as curvas C1: x² + y² = 16 e C2: x² + y² = 64 em um mesmo sistema de coordenadas cartesianas, é correto afirmar que uma circunferência tangente comum a essas curvas pode ter raio r e centro C tais que

A
r ∈ { 2, 6) e C ∈ { (x, y) / x² + y² = 4 }
B
r ∈ { 2, 6) e C ∈ { (x, y) / x² + y² = 36 }
C
r = 2 e C ∈ { (x, y)/ x² + y² = 4 }
D
r = 2 e C ∈ { (x, y)/ x² + y² = 36 } ou r = 6 e C ∈ { (x, y)/ x² + y² = 4 }
E
r = 2 e C ∈ { (x, y)/ x² + y² = 4 } ou r = 6 e C ∈ { (x, y) / x² + y² = 36 }
e5b2eb3a-e7
UEFS 2010 - Matemática - Áreas e Perímetros, Geometria Plana

As retas r e s, na figura, são paralelas e o ponto P, vértice do ângulo reto do triângulo PRS, está a 3√3 unidades de distância da reta r e a 4 unidades de distância da reta s.



Se a área do triângulo PRS mede 24u.a. então o seu perímetro mede, em unidades de comprimento

A
6√3
B
18 + 3√3
C
24
D
18 + √3
E
28
e5afe6f3-e7
UEFS 2010 - Matemática - Circunferências e Círculos, Trigonometria, Geometria Plana, Funções Trigonométricas e Funções Trigonométricas Inversas

Em um parque de diversões, uma roda gigante de raio r = 10m, tendo 12 cadeiras igualmente espaçadas ao longo de seu perímetro, faz uma volta completa em 30 segundos. Além disso, o ponto mais baixo atingido ao longo do percurso circular está a 0,5m do solo. Certo dia, depois de todos os assentos estarem ocupados, o assento 1 se encontrava na posição indicada na figura, quando a roda começa a girar no sentido anti-horário.



Sendo a distância desse assento ao solo, t segundos após a roda ter começado a girar, dada pela expressão D(t) =M+N sen(αt), α > 0, é correto afirmar que M − N é igual a

A
cos(5α)
B
sen(5α)
C
cos(10α)
D
sen(10α)
E
cos(15α)
a45b8e14-e3
UEFS 2011 - Matemática - Áreas e Perímetros, Geometria Plana

Na figura, os segmentos OR e PQ são lados paralelos do quadrilátero OPQR, e o vértice Q é o ponto em que a função f(x) = 2(−x2 + 4x) assume seu maior valor



Sendo a área da região sombreada igual a 18u.a., pode-se afirmar que uma equação cartesiana da reta r que contém o lado RQ do quadrilátero é

A
y − 5x − 4 = 0
B
y − 7x − 2 = 0
C
3y − 2x − 3 = 0
D
4y − x − 16 = 0
E
3y − 20x − 12 = 0
a460a3c0-e3
UEFS 2011 - Matemática - Circunferências e Círculos, Geometria Plana

Considere, no sistema de coordenadas cartesianas, uma circunferência que tangencia o eixo das ordenadas em y = √112 e também tangencia a reta √7y-3x = 0. Sabendo-se que nenhum ponto da circunferência tem coordenadas negativas, pode-se afirmar que a distância do centro da circunferência à origem é, em u.c., aproximadamente, igual a

A
8
B
9
C
10
D
11
E
12
a452c0d3-e3
UEFS 2011 - Matemática - Áreas e Perímetros, Geometria Plana

O quadrado e o círculo representados na figura têm centro no mesmo ponto e, nessa figura, as regiões sombreadas têm área de mesma medida.



Nessas condições, pode-se afirmar que

A
a área do círculo é igual à área do quadrado.
B
a área do círculo é menor do que a área do quadrado.
C
a área do círculo é maior do que a área do quadrado.
D
a relação entre as áreas do círculo e do quadrado depende da medida do lado do quadrado.
E
a relação entre as áreas do círculo e do quadrado depende da medida do raio da circunferência.
a44525d2-e3
UEFS 2011 - Matemática - Geometria Plana, Triângulos


Estudos mostraram a viabilidade da construção de uma ponte ligando uma cidade litorânea a uma ilha, a partir de um ponto P ou de um ponto Q da costa, distantes 2400m um do outro, até um ponto I da referida ilha.


Sabe-se que se a ponte for construída a partir de P ou de Q, formará com PQ ângulos de 45º e 60º, respectivamente, e que, nas duas situações, o custo de construção é de 100 unidades monetárias por metro linear.


Com base nessas informações e considerando-se sen 75º = 0,96, √2=1,4 e √3=1,7, pode-se afirmar que, optando-se pela construção da ponte menor, haverá uma economia, em unidades monetárias, de

A
12500
B
20350
C
37500
D
41330
E
51200
a44e454c-e3
UEFS 2011 - Matemática - Geometria Plana, Triângulos


O triângulo QRN, na figura, foi obtido, girando-se o triângulo MNO em torno do ponto N.


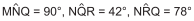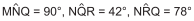Sabendo-se que e, considerando-se P o ponto de intersecção dos segmentos OR e QN, pode-se afirmar que o ângulo mede

A
95º
B
99º
C
102º
D
105º
E
108º
17bcfd0b-e3
UEFS 2011 - Matemática - Geometria Plana, Triângulos, Polinômios

As raízes do polinômio P(x) = x3 − 14x2 + 63x − 90 são medidas dos lados de um triângulo.


Nessas condições, a área desse triângulo, em u.a, é igual a

A
2√6
B
√10
C
2√10
D
√14
E
2√14
17acb731-e3
UEFS 2011 - Matemática - Geometria Plana, Triângulos


Na figura em evidência, ABC é um triângulo equilátero de 12cm de lado. Além disso, M é o ponto médio de AC e BE = 12cm.


Nessas condições, a medida do segmento BN, em cm, é igual a


A
2
B
3
C
4
D
5
E
6
17a8d67c-e3
UEFS 2011 - Matemática - Circunferências e Círculos, Polígonos, Geometria Plana

Na figura ao lado, ABCD é um quadrado de lado a. A circunferência de raio x tangencia os lados AB e AD e a semicircunferência de diâmetro CD.




O valor de x em função de a é

A


B


C


D


E


17aff288-e3
UEFS 2011 - Matemática - Geometria Plana, Triângulos

Sejam 5x − 5, 3x − 2 e x + 4 as medidas dos lados de um triângulo.


Se x é um número inteiro, o número de triângulos, obtusângulos e escalenos, distintos, que podem ser formados, satisfazendo-se as medidas referidas, é igual a

A
1
B
2
C
3
D
4
E
5