Questõesde PUC - PR sobre Geometria Plana
Um triângulo possui uma circunferência inscrita e outra circunscrita. Um dos lados do triângulo passa
pelo centro da circunferência circunscrita e a soma das medidas dos outros lados é igual a s. Qual é a
medida da soma dos comprimentos das duas circunferências?
O termo acessibilidade significa incluir a pessoa com deficiência na participação de atividades. Um exemplo é o acesso para cadeira de rodas através de rampas. A Associação Brasileira de Normas Técnicas (ABNT) regulamentou a construção dessas rampas.A inclinação com o plano horizontal deve variar de 5% a 8,33%, de acordo com a tabela abaixo.

Suponha que seja preciso construir uma rampa para um desnível cuja altura é de 0,90m. De quando deve ser o afastamento mínimo, a fim de que essa rampa figue de acordo com o regulamento estabelecido pela ABNT?
O termo acessibilidade significa incluir a pessoa com deficiência na participação de atividades. Um exemplo é o acesso para cadeira de rodas através de rampas. A Associação Brasileira de Normas Técnicas (ABNT) regulamentou a construção dessas rampas.A inclinação com o plano horizontal deve variar de 5% a 8,33%, de acordo com a tabela abaixo.

Suponha que seja preciso construir uma rampa para um desnível cuja altura é de 0,90m. De quando deve ser o afastamento mínimo, a fim de que essa rampa figue de acordo com o regulamento estabelecido pela ABNT?
De um icoságono regular são escolhidos dois vértices. Qual a probabilidade de que o segmento formado seja uma
diagonal que passe pelo centro do icoságono?
Um topógrafo deseja medir a distância x de um ponto Q na margem de um rio até um ponto inacessível P
na outra margem, conforme a figura. Sabendo-se que ele visualiza o ponto P segundo um ângulo β e, em
seguida, ele se desloca uma distância b até o ponto R e observa o ponto P segundo o ângulo θ, a expressão
que calcula a distância x é







As soluções (valores de z) na equação zn = K, sendo 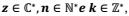 são pontos de uma
circunferência. Calcule a área do setor circular
formado nessa circunferência, tal que as
extremidades do arco que forma o setor sejam duas
soluções consecutivas da equação.
são pontos de uma
circunferência. Calcule a área do setor circular
formado nessa circunferência, tal que as
extremidades do arco que forma o setor sejam duas
soluções consecutivas da equação.
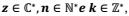 são pontos de uma
circunferência. Calcule a área do setor circular
formado nessa circunferência, tal que as
extremidades do arco que forma o setor sejam duas
soluções consecutivas da equação.
são pontos de uma
circunferência. Calcule a área do setor circular
formado nessa circunferência, tal que as
extremidades do arco que forma o setor sejam duas
soluções consecutivas da equação.
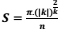



Se θ e φ são os ângulos agudos de um triângulo retângulo, calcule o valor da expressão 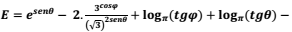
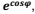 sabendo que π é uma constante de valor aproximado de 3,1417 e e é uma constante de valor aproximado de 2,71.
sabendo que π é uma constante de valor aproximado de 3,1417 e e é uma constante de valor aproximado de 2,71.
Se θ e φ são os ângulos agudos de um triângulo retângulo, calcule o valor da expressão 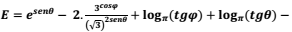
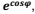 sabendo que π é uma constante de valor aproximado de 3,1417 e e é uma constante de valor aproximado de 2,71.
sabendo que π é uma constante de valor aproximado de 3,1417 e e é uma constante de valor aproximado de 2,71.
. A espiral abaixo representa as ruas AB, BC, CD, DE e
EF de uma cidade.
Uma pessoa se encontra no ponto A e precisa chegar
no ponto F fazendo a seguinte rota:

Sabe-se que, nessa sequência, a medida de cada rua
corresponde a 75% da medida da rua anterior.

Se 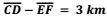 , então, a rua
, então, a rua 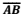 , em
quilômetros, mede:
, em
quilômetros, mede:
. A espiral abaixo representa as ruas AB, BC, CD, DE e EF de uma cidade.
Uma pessoa se encontra no ponto A e precisa chegar no ponto F fazendo a seguinte rota:

Sabe-se que, nessa sequência, a medida de cada rua corresponde a 75% da medida da rua anterior.

Se 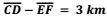 , então, a rua
, então, a rua 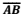 , em
quilômetros, mede:
, em
quilômetros, mede: