Questõesde UFRGS sobre Geometria Espacial

InícioTodas as questões
1
1
1
Foram encontradas 14 questões
9451a72b-05
UFRGS 2016 - Matemática - Geometria Espacial, Cilindro

Em uma caixa, há sólidos geométricos, todos de mesma altura: cubos, cilindros, pirâmides quadrangulares regulares e cones. Sabe-se que as arestas da base dos cubos e das pirâmides têm a mesma medida; que o raio da base dos cones e dos cilindros tem a mesma medida. Somando o volume de 2 cubos e de 2 cilindros, obtêm-se 180 cm³ . A soma dos volumes de 3 cubos e 1 cone resulta em 110 cm³ , e a soma dos volumes de 2 cilindros e 3 pirâmides resulta em 150 cm³.

O valor da soma dos volumes, em cm³ , de um cubo, um cilindro, dois cones e duas pirâmides é

A
150.
B
160.
C
190.
D
210.
E
240.
943e2aae-05
UFRGS 2016 - Matemática - Análise de Tabelas e Gráficos, Cone, Geometria Espacial

Um recipiente tem a forma de um cone com o vértice para baixo, como na figura a seguir.


Para encher de água esse recipiente, será aberta uma torneira com vazão constante de água.

Assinale o gráfico abaixo que melhor representa a altura y que a água atinge, no recipiente, em função do tempo x.

A

B

C

D


E

943b3af8-05
UFRGS 2016 - Matemática - Geometria Espacial, Poliedros

Considere ABCDEFGH um paralelepípedo retoretângulo conforme representado na figura abaixo.


Se as arestas do paralelepípedo medem 3, 6 e 10, o volume do sólido ACDH é

A
10.
B
20.
C
30.
D
60.
E
90.
942bb15a-05
UFRGS 2016 - Matemática - Geometria Espacial, Poliedros

Uma caixa com a forma de um paralelepípedo retangular tem as dimensões dadas por

x , x + 4 e x - 1.

Se o volume desse paralelepípedo é 12, então as medidas das dimensões da caixa são

A
1, 1 e 12.
B
1, 2 e 6.
C
1, 3 e 4.
D
2, 2 e 3
E
2, 3 e 4.
cef8d9ff-fa
UFRGS 2019 - Matemática - Aritmética e Problemas, Pirâmides, Razão, Proporção e Números Proporcionais, Geometria Espacial, Poliedros

Considere o cubo e os tetraedros ABCD, EFGD e HIJD, nos quais os pontos A, C, E, G, H e J são pontos médios de arestas do cubo, como representado na figura abaixo.




A razão entre a soma dos volumes dos tetraedros ABCD, EFGD e HIJD e o volume do cubo é

A
1/8.
B
1/6.
C
1/3.
D
2/3.
E
3/4.
eb792c02-af
UFRGS 2017 - Matemática - Geometria Plana, Triângulos, Geometria Espacial, Poliedros

Considere a planificação de um tetraedro, conforme a figura abaixo.



Os triângulos ABC e ABD são isósceles respectivamente em B e D. As medidas dos segmentos estão indicadas na figura.


A soma das medidas de todas as arestas do tetraedro é

A
33.
B
34.
C
43.
D
47.
E
48.
eb74fb05-af
UFRGS 2017 - Matemática - Geometria Espacial, Poliedros

Considere ABCDEFGH paralelepípedo retoretângulo, indicado na figura abaixo, tal que .



O volume do tetraedro AHFC é

A
4.
B
8.
C
12.
D
16.
E
18.
eb7eaadf-af
UFRGS 2017 - Matemática - Geometria Espacial, Poliedros

Considere um cubo de aresta a. Os pontos I, J, K, L, M e N são os centros das faces ABCD, BCGF, DCGH, ADHE, ABFE e EFGH, respectivamente, conforme representado na figura abaixo.



O octaedro regular, cujos vértices são os pontos I, J, K, L, M e N, tem aresta medindo

A
a√3 .
B
a√2 .
C



D


E

eb6d9900-af
UFRGS 2017 - Matemática - Geometria Espacial, Poliedros

Considere um pentágono regular ABCDE de lado 1. Tomando os pontos médios de seus lados, constrói-se um pentágono FGHIJ, como na figura abaixo.



A medida do lado do pentágono FGHIJ é

A
sen 36° .
B
cos 36° .
C
sen 36°/2 .
D
cos 36°/2 .
E
2 cos 36° .
d13c0e6d-ba
UFRGS 2019 - Matemática - Geometria Espacial, Poliedros

Na figura a seguir, está representado um cubo cuja aresta tem 2 cm de medida. O ponto P está localizado no centro da face EFGH .



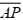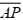A medida do segmento é

NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:

N: Conjunto dos números naturais.

R: Conjunto dos números reais.

A
√2.
B
2 .
C
√6 .
D
2√3 .
E
3 .
d137ff5f-ba
UFRGS 2019 - Matemática - Geometria Espacial, Poliedros

Considere o sólido obtido pela revolução do retângulo ABCD em torno da reta r , conforme indicado na figura a seguir.



O volume do sólido obtido é

NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:

N: Conjunto dos números naturais.

R: Conjunto dos números reais.

A
16π.
B
84.
C
100.
D
84π.
E
100π.
d1340675-ba
UFRGS 2019 - Matemática - Pirâmides, Geometria Espacial

Considere o paralelepípedo de vértices A, B, C, D, E, F, G, H e a pirâmide de vértices B, F, G, H, inscrita no paralelepípedo, representados na figura a seguir.



A razão entre o volume da pirâmide e o volume do paralelepípedo é

NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:

N: Conjunto dos números naturais.

R: Conjunto dos números reais.

A
1/6 .
B
1/5 .
C
1/4 .
D
1/3 .
E
1/2 .
76fb1634-cc
UFRGS 2018 - Matemática - Prismas, Geometria Espacial

Uma partícula parte do ponto A e chega ao ponto H percorrendo a poligonal ABCDEFGH no cubo de aresta unitária, representado na figura abaixo.



A distância percorrida pela partícula é

A
1 .
B
√2 .
C
7 .
D
5 + 2√2 .
E
5 + 2√3 .
76f3a958-cc
UFRGS 2018 - Matemática - Esfera, Geometria Espacial

Fundindo três esferas idênticas e maciças de diâmetro 2 cm, obtém-se uma única esfera maciça de raio

A
∛3 .
B
∛4.
C
∛6.
D
3.
E
6.