Sabendo que as retas r // s, o valor
do ângulo x é:

Sabendo que as retas r // s, o valor do ângulo x é:

Sabendo que as retas r // s, o valor do ângulo x é:


As equações
y=2x+3 ,
2x+y-5=0, e
x2 + y2 =25
representam no plano cartesiano, respectivamente





Uma circunferência tangencia o lado BC de um triângulo ABC no ponto F e intersecta os lados AB e AC desse triângulo, nos pontos E e D respectivamente, conforme mostra a figura.

Sabendo que essa circunferência passa pelo
ponto A, a distância entre os pontos D e E, em
cm, é igual a

Considere que os quarteirões de um bairro tenham sido desenhados no sistema cartesiano, sendo a origem o cruzamento das duas ruas mais movimentadas desse bairro. Nesse desenho, as ruas têm suas larguras desconsideradas e todos os quarteirões são quadrados de mesma área e a medida de seu lado é a unidade do sistema.
A seguir, há uma representação dessa situação, em que os pontos A, B, C e D representam estabelecimentos comerciais desse bairro.

Suponha que uma estação de rádio comunitária, de fraco sinal, garante área de cobertura para todo estabelecimento que se encontra num ponto cujas coordenadas satisfaçam à inequação:

A fim de avaliar a qualidade do sinal e proporcionar uma futura melhora, a assistência técnica da rádio realizou uma inspeção para saber quais estabelecimentos estavam dentro da área de cobertura, pois estes conseguem ouvir a rádio, enquanto os outros não.
Os estabelecimentos que conseguem ouvir a rádio são apenas:
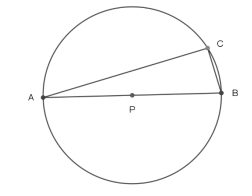
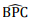 mede π/6 radianos, e o ponto é o centro da
circunferência de raio 3. A área do triângulo ABC, em unidades de área, é
mede π/6 radianos, e o ponto é o centro da
circunferência de raio 3. A área do triângulo ABC, em unidades de área, é