Na fi gura a seguir, ABCD é um retângulo e o
ponto E é a interseção dos segmentos 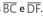 .
Se BE = 2; CE, EF = 2; DE, AB = 4 cm e
AD = 9 cm, qual das medidas a seguir
mais se aproxima de CF?
.
Se BE = 2; CE, EF = 2; DE, AB = 4 cm e
AD = 9 cm, qual das medidas a seguir
mais se aproxima de CF?

Na fi gura a seguir, ABCD é um retângulo e o
ponto E é a interseção dos segmentos 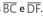 .
Se BE = 2; CE, EF = 2; DE, AB = 4 cm e
AD = 9 cm, qual das medidas a seguir
mais se aproxima de CF?
.
Se BE = 2; CE, EF = 2; DE, AB = 4 cm e
AD = 9 cm, qual das medidas a seguir
mais se aproxima de CF?






 7
7






